Question

Find the area of the greatest of isosceles triangles that can be inscribed in a given ellipse having its vertex coincide with one end of the major axis?

Answer 1

Hint: Consider the general equation of the ellipse. Draw the triangle inscribed in an ellipse, as the ellipse is symmetrical the 2 opposite vertices will have similar coordinates. Thus find the area of the triangle, differentiate the obtained equation, take $z={{A}^{2}}$.

Complete step-by-step answer:
Let us consider the general equation of ellipse is,
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$

The major axis of the ellipse is AA’, which is along the x-axis. We know that the length of the major axis = 2a.
$\therefore AA'=2a$.
Thus from the figure, we can say that OA’ = OA = a.
Hence we can form the coordinates of A as (a, 0).
An isosceles triangle inscribed in the ellipse it in the ellipse its vertex at one end of the major axis. Let $\Delta PAP'$ be an isosceles triangle.
Thus the coordinates of P can be taken as (h, k) and coordinates of P’ (h, -k) as the ellipse is symmetric.
We need to find the greatest area of the triangle.
Let A be the area of the isosceles triangle $\Delta PAP'$.
We know the area of the isosceles triangle $\Delta PAP'$.
We know the area of the triangle = $\dfrac{1}{2}\times$ base $\times$ height.
$A=\dfrac{1}{2}\times PP'\times AM$, (From the figure)

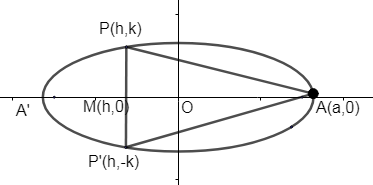
Let us consider a point M which lies on the x-axis. Thus the coordinates of M are (h, 0) as it lies on the x-axis.
Since point (h, k) lie on the ellipse.
$\therefore$ (h, k) will satisfy the equation of ellipse.
Let us put x = h and y = k in the equation of ellipse.
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
$\therefore \dfrac{{{\left( h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( k \right)}^{2}}}{{{b}^{2}}}=1$
By simplifying the expression,
$\Rightarrow \dfrac{{{h}^{2}}{{b}^{2}}+{{k}^{2}}{{a}^{2}}}{{{a}^{2}}{{b}^{2}}}=1$
Cross multiply the above,

& {{h}^{2}}{{b}^{2}}+{{k}^{2}}{{a}^{2}}={{a}^{2}}{{b}^{2}} \\\ & \therefore {{a}^{2}}{{k}^{2}}={{a}^{2}}{{b}^{2}}-{{b}^{2}}{{h}^{2}} \\\ \end{aligned}$$ $${{k}^{2}}=\dfrac{{{a}^{2}}{{b}^{2}}-{{b}^{2}}{{h}^{2}}}{{{a}^{2}}}$$ $$\therefore k=\sqrt{\dfrac{{{a}^{2}}{{b}^{2}}-{{b}^{2}}{{h}^{2}}}{{{a}^{2}}}}=\dfrac{1}{a}\sqrt{{{\left( ab \right)}^{2}}-{{\left( bh \right)}^{2}}}-(1)$$ We know the values, P (h, k), P’ (h, -k), A (a, 0) and M (h, 0). Now let us find PP’. We can use the distance formula to find the distance which is given by $$\begin{aligned} & \sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} \\\ & \therefore PP'=\sqrt{{{\left( h-h \right)}^{2}}+{{\left( -k-k \right)}^{2}}}=\sqrt{0+{{\left( -2k \right)}^{2}}}=\sqrt{4{{k}^{2}}} \\\ & \therefore PP'=2k \\\ \end{aligned}$$ Similarly let us find AM using distance formula. $$\begin{aligned} & AM=\sqrt{{{\left( a-h \right)}^{2}}+{{\left( 0-0 \right)}^{2}}} \\\ & AM=\sqrt{{{\left( a-h \right)}^{2}}} \\\ & AM=a-h \\\ \end{aligned}$$ Thus we found the area of the triangle as, $$A=\dfrac{1}{2}\times PP'\times AM$$. $$\therefore A=\dfrac{1}{2}\times \left( a-h \right)\times 2k=\left( a-h \right)k$$ From equation (1), substitute the value of k to the above expression, $$A=\dfrac{\left( a-h \right)}{a}\sqrt{{{\left( ab \right)}^{2}}-{{\left( bh \right)}^{2}}}$$ Let us consider, $$z={{A}^{2}}$$. $$\begin{aligned} & \therefore z={{\left[ \left( \dfrac{a-h}{a} \right)\sqrt{{{\left( ab \right)}^{2}}-{{\left( bh \right)}^{2}}} \right]}^{2}} \\\ & z=\dfrac{{{\left( a-h \right)}^{2}}}{{{a}^{2}}}\left[ {{\left( ab \right)}^{2}}-{{\left( bh \right)}^{2}} \right] \\\ \end{aligned}$$ $$z=\dfrac{{{\left( a-h \right)}^{2}}}{{{a}^{2}}}\times {{b}^{2}}\left[ {{a}^{2}}-{{h}^{2}} \right]$$ $$z={{\left( \dfrac{b}{a} \right)}^{2}}{{\left( a-h \right)}^{2}}\left( {{a}^{2}}-{{h}^{2}} \right)$$ Now let us differentiate the above expression with respect to h. $$\begin{aligned} & \dfrac{dz}{dh}=\dfrac{d}{dh}\left[ {{\left( \dfrac{b}{a} \right)}^{2}}{{\left( a-h \right)}^{2}}\left( {{a}^{2}}-{{h}^{2}} \right) \right] \\\ & \dfrac{dz}{dh}={{\left( \dfrac{b}{a} \right)}^{2}}\dfrac{d}{dh}\left[ {{\left( a-h \right)}^{2}}\left( {{a}^{2}}-{{h}^{2}} \right) \right] \\\ \end{aligned}$$ Now let us use the product rule, as $$uv=u'v+v'u$$ $$\begin{aligned} & \dfrac{dz}{dh}={{\left( \dfrac{b}{a} \right)}^{2}}\left[ \dfrac{d}{dh}{{\left( a-h \right)}^{2}}.\left( {{a}^{2}}-{{h}^{2}} \right)+\dfrac{d}{dh}\left( {{a}^{2}}-{{h}^{2}} \right).{{\left( a-h \right)}^{2}} \right] \\\ & \dfrac{dz}{dh}={{\left( \dfrac{b}{a} \right)}^{2}}\left[ 2\left( a-h \right)\left( -1 \right)\left( {{a}^{2}}-{{h}^{2}} \right)+\left( 0-2h \right){{\left( a-h \right)}^{2}} \right] \\\ & \dfrac{dz}{dh}={{\left( \dfrac{b}{a} \right)}^{2}}\left[ -2\left( a-h \right)\left( {{a}^{2}}-{{h}^{2}} \right)-2h{{\left( a-h \right)}^{2}} \right] \\\ & \dfrac{dz}{dh}={{\left( \dfrac{b}{a} \right)}^{2}}\left( -2 \right)\left( a-h \right)\left[ {{a}^{2}}-{{h}^{2}}+ha-{{h}^{2}} \right] \\\ & \dfrac{dz}{dh}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left( a-h \right)\left[ {{a}^{2}}+ha-2{{h}^{2}} \right] \\\ \end{aligned}$$ Let us put, $$\dfrac{dz}{dh}=0$$. $$\begin{aligned} & -2{{\left( \dfrac{b}{a} \right)}^{2}}\left( a-h \right)\left[ {{a}^{2}}+ha-2{{h}^{2}} \right]=0 \\\ & \therefore \left( a-h \right)\left( {{a}^{2}}+ah-2{{h}^{2}} \right)=0 \\\ \end{aligned}$$ From the above expression, we know that $$a-h=0$$ and $${{a}^{2}}+ah-2{{h}^{2}}=0$$ Thus by solving, $$a-h=0$$, we get, a = h. $${{a}^{2}}+ah-2{{h}^{2}}=0$$, add and subtract ah in this expression. $$\begin{aligned} & {{a}^{2}}+ah-2{{h}^{2}}+ah-ah=0 \\\ & {{a}^{2}}+2ah-2{{h}^{2}}-ah=0 \\\ & {{a}^{2}}+2ah-ah-2{{h}^{2}}=0 \\\ & a\left( a+2h \right)-h\left( a+2h \right)=0 \\\ & \left( a-h \right)\left( a+2h \right)=0 \\\ \end{aligned}$$ $$\therefore a-h=0$$ and $$a+2h=0$$. $$\therefore h=a$$ and $$h=\dfrac{-a}{2}$$. Thus we get h = a and $$h=\dfrac{-a}{2}$$. If h = a, $$\therefore k=\dfrac{1}{a}\sqrt{{{\left( ab \right)}^{2}}-{{\left( bh \right)}^{2}}}$$ $$k=\dfrac{1}{a}\sqrt{{{\left( ab \right)}^{2}}-{{\left( bh \right)}^{2}}}=0$$, but this is not possible. So, let us find $$\dfrac{{{d}^{2}}z}{d{{h}^{2}}}$$, w.r.t ‘h’. $$\begin{aligned} & \dfrac{dz}{dh}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ \left( a-h \right)\left( {{a}^{2}}+ah-2{{h}^{2}} \right) \right] \\\ & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\dfrac{d}{dh}\left[ \left( a-h \right)\left( {{a}^{2}}+ah-2{{h}^{2}} \right) \right] \\\ \end{aligned}$$ Use the product rule to solve, $$uv=u'v+v'u$$. $$\begin{aligned} & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ \dfrac{d}{dh}\left( a-h \right)\left( {{a}^{2}}+ah-2{{h}^{2}} \right)+\dfrac{d}{dh}\left( {{a}^{2}}+ah-2{{h}^{2}} \right)\left( a-h \right) \right] \\\ & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ \left( -1 \right)\left( {{a}^{2}}+ah-2{{h}^{2}} \right)+\left( a-4h \right)\left( a-h \right) \right] \\\ & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ -{{a}^{2}}-ah+2{{h}^{2}}+{{a}^{2}}-ah-4ah+4{{h}^{2}} \right] \\\ \end{aligned}$$ Open the brackets and simplify the expression, $$\dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ -2ah-4ah+6{{h}^{2}} \right]$$ Now let us put, $$h=\dfrac{-a}{2}$$. $$\begin{aligned} & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ -2a\left( \dfrac{-a}{2} \right)-4a\left( \dfrac{-a}{2} \right)+6{{\left( \dfrac{-a}{2} \right)}^{2}} \right] \\\ & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ {{a}^{2}}+2{{a}^{2}}+\dfrac{3}{2}{{a}^{2}} \right] \\\ & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ \dfrac{9{{a}^{2}}}{2} \right]=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left( \dfrac{9{{a}^{2}}}{2} \right) \\\ & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-9{{b}^{2}}<0 \\\ \end{aligned}$$ $$\dfrac{{{d}^{2}}z}{d{{h}^{2}}}<0$$ at $$h=\dfrac{-a}{2}$$. Therefore z is maximum when, $$h=\dfrac{-a}{2}$$. Thus the area will be maximum when, $$h=\dfrac{-a}{2}$$. Let us put $$h=\dfrac{-a}{2}$$, in equation (1). $$\begin{aligned} & k=\dfrac{1}{a}\sqrt{{{\left( ab \right)}^{2}}-{{\left( bh \right)}^{2}}} \\\ & k=\dfrac{1}{a}\sqrt{{{\left( ab \right)}^{2}}-{{b}^{2}}{{\left( \dfrac{-a}{2} \right)}^{2}}} \\\ & k=\dfrac{1}{a}\sqrt{{{\left( ab \right)}^{2}}-\dfrac{{{a}^{2}}{{b}^{2}}}{4}}=\dfrac{ab}{a}\sqrt{1-\dfrac{1}{4}} \\\ & k=b\sqrt{\dfrac{4-1}{4}}=\dfrac{b\sqrt{3}}{2} \\\ \end{aligned}$$ Hence, we have $$h=\dfrac{-a}{2}$$ and $$k=\dfrac{b\sqrt{3}}{2}$$. We need to find the maximum value of Area. $$\begin{aligned} & A=\dfrac{1}{2}\times \left( a-h \right)\left( 2k \right) \\\ & A=\dfrac{1}{2}\left( a-\left( \dfrac{-a}{2} \right) \right)\times 2\left( \dfrac{b\sqrt{3}}{2} \right) \\\ & A=\dfrac{1}{2}\left( a+\dfrac{a}{2} \right)b\sqrt{3} \\\ & A=\dfrac{1}{2}\left( \dfrac{3a}{2} \right)b\sqrt{3} \\\ & A=\dfrac{3\sqrt{3}ab}{4} \\\ \end{aligned}$$ Hence, we got the maximum area $$=\dfrac{3\sqrt{3}ab}{4}$$. Note: We did differentiation two times in $$\dfrac{dz}{dh}$$, we got the value of k as zero. If k was not zero than $$\dfrac{{{d}^{2}}z}{d{{h}^{2}}}$$ is not required to get the value of k. thus find the coordinates (h, k) and find the area. Here $$\dfrac{{{d}^{2}}z}{d{{h}^{2}}}$$ should be less than zero.