Question

Find the area of the given triangle whose angles are ${30^ \circ },{60^ \circ },{90^ \circ }$?

Answer 1

For finding the area of a given triangle you need to have the measurement of the sides, which can be calculated by the given angles or of given in the question already. For finding the sides you have to use the trigonometry identity to find the values as we already know the trigonometry values for a given angle.

Formulae Used: $Area = \dfrac{1}{2} \times base \times height$,$\tan \theta = \dfrac{{perpendicular}}{{base}}$,$\tan 60 = \sqrt 3$

Complete step by step solution:
The given angles are ${30^ \circ },{60^ \circ },{90^ \circ }$
Let's draw a triangle with the given angles and assume variables for the length of sides which needed to be obtained for further finding the area of the triangle:

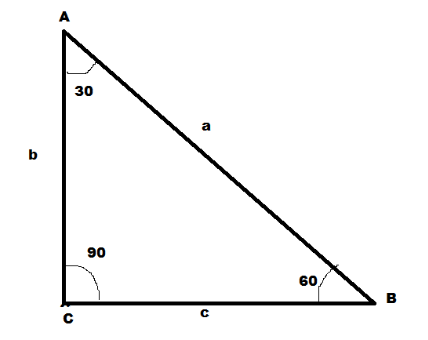
For the above triangle area of the triangle can be find by using formula:
$\dfrac{1}{2} \times base \times height$

Here base of the triangle is “CB” whose length is “c” and height of the triangle is “AC” whose length is “b”

To find both the length we can use:
$\tan \theta = \dfrac{{perpendicular}}{{base}} = \dfrac{{AC}}{{CB}}(for\,our\,given\,triangle)$
Here the value of angle $\theta$ is “60 degree”

Now using above formulae we get;

$$\tan 60 = \dfrac{{AC}}{{CB}} \\\ \sqrt 3 = \dfrac{{AC}}{{CB}}(\tan 60 = \sqrt 3 ) \\\ we\,get;\,AC = \sqrt 3 \,and\,CB = 1;\,on\,comparison\,on\,both\,sides\,of\,equation \\\$$

So area of the given triangle is:

$$Area = \dfrac{1}{2} \times base \times height \\\ Area = \dfrac{1}{2} \times AC \times CB \\\ Area = \dfrac{1}{2} \times \sqrt 3 \times 1 \\\ Area = \dfrac{{1.731}}{2}\,(\sqrt 3 = 1.732) \\\ Area = 0.866\,sq\,units \\\$$

Our required area for the given triangle is $0.866\,sq\,units$.

Note: Here we are to use the “sin” values to find the measurement of the sides but you can use any other trigonometric identity according to your ease. The only result we want is the measurement of the sides; it is up to us how we are going to find it and which identity suits best according to the data given in the question.