Question

Find the area of the circle $4{{x}^{2}}+4{{y}^{2}}=9$ which is interior to the parabola ${{x}^{2}}=4y$.

Answer 1

Find the intersection of the given circle and parabola. Get the bounded area with the help of a neat sketch. Area of f(x) with the x-axis from x = a to x = b is given as
$\int\limits_{a}^{b}{f\left( x \right)}dx$
Use the relation
$\int{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{a} \right)$

Complete answer:
We have equation of circle as $4{{x}^{2}}+4{{y}^{2}}=9$ and equation of parabola as ${{x}^{2}}=4y$. And we need to determine the area formed between the interior of them.
So, we need to draw the diagram representing both the curves.
So, we can compare equation of circle with the standard equation of circle i.e. given as
${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{C}^{2}}$ ……….. (i)
Where $\left( {{x}_{1}},{{y}_{1}} \right)$are centre and C is the radius.
So, equation of circle in problem is
$4{{x}^{2}}+4{{y}^{2}}=9,{{x}^{2}}+{{y}^{2}}=\dfrac{9}{4}$
${{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}={{\left( \dfrac{3}{2} \right)}^{2}}$………….. (ii)
Now, compare this equation with the standard equation of the circle given in equation (i). we get
Centre = (0,0)
Radius = $\dfrac{3}{2}$
And compare the equation of parabola ${{x}^{2}}=4y\to {{x}^{2}}=4ay$, and get that vertex of this parabola is (0,0). So, we get diagram as

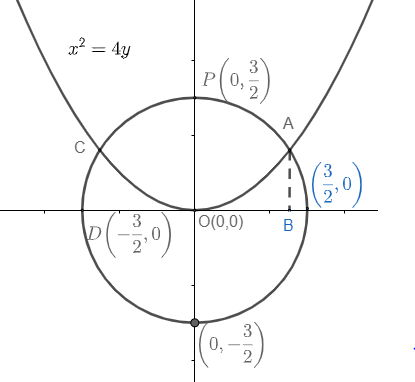
So, we need to calculate the area of the region OCPAO. It can be calculated adding areas of OCPO and OAPO, and both areas i.e. area of OCPO and OAPO will be equal to each other by the symmetry (as circle and parabola both are symmetric about y-axis). So, the area of shaded region OCPAO will be twice of OPAO and the area of OPAO will be the difference of area of OPAB and area of OAB.
So, let us find the intersection of the parabola and circle given in the question. So, we have equations of them as
$4{{x}^{2}}+4{{y}^{2}}=9$…………… (i)
${{x}^{2}}=4y$ ……………… (ii)
Put value of ${{x}^{2}}=4y$from equation (ii) to equation (i).Hence, we get
$\begin{aligned} & 4\left( 4y \right)+4{{y}^{2}}=9 \\\ & 16y+4{{y}^{2}}=9,4{{y}^{2}}+16y-9=0 \\\ & \\\ \end{aligned}$
Now, we can factorize this equation as
$\begin{aligned} & 4{{y}^{2}}+18y-2y-9=0 \\\ & 2y\left( 2y+9 \right)-1\left( 2y+9 \right)=0 \\\ & \left( 2y-1 \right)\left( 2y+9 \right)=0 \\\ \end{aligned}$
2y – 1 = 0, 2y + 9 = 0
$y=\dfrac{1}{2},y=-\dfrac{9}{2}$
As, we need to find point A which is lying in the first quadrant, so, the value of ‘y’ will be $\dfrac{1}{2}$. Hence, put $y=\dfrac{1}{2}$ to equation (ii); so, we get
$\begin{aligned} & {{x}^{2}}=4\times \dfrac{1}{2}=2 \\\ & x=\pm \sqrt{2} \\\ \end{aligned}$
So, the value of x will be $\sqrt{2}$, as coordinates of point A cannot be negative, as it is lying in the 1st quadrant. So, we get point A as $\left( \sqrt{2,}\dfrac{1}{2} \right)$.
So, the line AB will be represented as $x=\sqrt{2}$. Hence, we can divide the area of OPAB and the area of OAB by integrating the circle and parabola from x = 0 to $x=\sqrt{2}$.
So, we get
Area of OPAO = area of OPAB – area of OAB.
Value of y from equation of circle is given as
$4{{x}^{2}}+4{{y}^{2}}=9$
$\begin{aligned} & 4{{y}^{2}}=9-4{{x}^{2}} \\\ & {{y}^{2}}=\dfrac{9-4{{x}^{2}}}{4} \\\ & y=\sqrt{\dfrac{9-4{{x}^{2}}}{4}} \\\ \end{aligned}$
$y=\dfrac{1}{2}\sqrt{9-4{{x}^{2}}}$ ……………. (iii)
Value of y from of parabola is
$y=\dfrac{{{x}^{2}}}{4}$ ………….. (iv)
So, we get
Area of region OPAO = $\int\limits_{0}^{\sqrt{2}}{\dfrac{1}{2}}\sqrt{9-4{{x}^{2}}}-\int\limits_{0}^{\sqrt{2}}{\dfrac{{{x}^{2}}}{4}}dx$
$=\dfrac{1}{2}\int\limits_{0}^{\sqrt{2}}{\sqrt{{{\left( 3 \right)}^{2}}-{{\left( 2x \right)}^{2}}}}-\dfrac{1}{4}\int\limits_{0}^{\sqrt{2}}{{{x}^{2}}}dx$
As we know
$\begin{aligned} & \int{\sqrt{{{a}^{2}}-{{x}^{2}}}}dx=\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{a} \right) \\\ & \int{{{x}^{n}}}dx=\dfrac{{{x}^{n+1}}}{n+1} \\\ \end{aligned}$
So, we get
Area of region OPAO

& =\dfrac{1}{2}\int\limits_{0}^{\sqrt{2}}{2\sqrt{{{\left( \dfrac{3}{2} \right)}^{2}}-{{x}^{2}}}}-\dfrac{1}{4}\int\limits_{0}^{\sqrt{2}}{{{x}^{2}}}dx \\\ & =\int\limits_{0}^{\sqrt{2}}{2\sqrt{{{\left( \dfrac{3}{2} \right)}^{2}}-{{x}^{2}}}}-\dfrac{1}{4}\int\limits_{0}^{\sqrt{2}}{{{x}^{2}}}dx \\\ \end{aligned}$$ Now, use the above mentioned results of integrals. So, we get Area of region OPAO $$\begin{aligned} & ={{\left( \dfrac{x}{2}\sqrt{{{\left( \dfrac{3}{2} \right)}^{2}}-{{x}^{2}}}+{{\left( \dfrac{3}{2} \right)}^{2}}\times \dfrac{1}{2}\times {{\sin }^{-1}}\left( \dfrac{x}{\left( \dfrac{3}{2} \right)} \right) \right)}_{0}}^{\sqrt{2}}-\dfrac{1}{4}{{\left( \dfrac{{{x}^{3}}}{3} \right)}_{0}}^{\sqrt{2}} \\\ & =\dfrac{\sqrt{2}}{2}\sqrt{\dfrac{9}{4}-2}+\dfrac{9}{8}{{\sin }^{-1}}\dfrac{2}{3}\sqrt{2}-\dfrac{1}{4}\dfrac{{{\sqrt{2}}^{3}}}{3} \\\ & =\dfrac{1}{\sqrt{2}}\times \dfrac{1}{2}+\dfrac{9}{8}{{\sin }^{-1}}\dfrac{2\sqrt{2}}{3}-\dfrac{2\sqrt{2}}{12} \\\ & =\dfrac{1}{2\sqrt{2}}+\dfrac{9}{8}{{\sin }^{-1}}\dfrac{2\sqrt{2}}{3}-\dfrac{\sqrt{2}}{6} \\\ & =\dfrac{1}{2\sqrt{2}}-\dfrac{\sqrt{2}}{6}+\dfrac{9}{8}{{\sin }^{-1}}\left( \dfrac{2\sqrt{2}}{3} \right) \\\ & =\dfrac{\sqrt{2}}{4}-\dfrac{\sqrt{2}}{6}+\dfrac{9}{8}{{\sin }^{-1}}\left( \dfrac{2\sqrt{2}}{3} \right) \\\ & =\dfrac{\sqrt{2}}{12}+\dfrac{9}{8}{{\sin }^{-1}}\left( \dfrac{2\sqrt{2}}{3} \right) \\\ & =\dfrac{1}{6\sqrt{2}}+\dfrac{9}{8}{{\sin }^{-1}}\left( \dfrac{2\sqrt{2}}{3} \right) \\\ \end{aligned}$$ Hence, we get area of region OPAO $$=\dfrac{1}{6\sqrt{2}}+\dfrac{9}{8}{{\sin }^{-1}}\left( \dfrac{2\sqrt{2}}{3} \right)$$ Hence, the area of the shaded region will be just double the area of OPAO. So, we get Area of shaded region $\begin{aligned} & =2\times \left( \dfrac{1}{6\sqrt{2}}+\dfrac{9}{8}{{\sin }^{-1}}\left( \dfrac{2\sqrt{2}}{3} \right) \right) \\\ & =\dfrac{1}{3\sqrt{2}}+\dfrac{9}{4}{{\sin }^{-1}}\left( \dfrac{2\sqrt{2}}{3} \right) \\\ \end{aligned}$ **Note:** Another approach for the question would be that we can calculate the area of the shaded region fromWe can get the area of the shaded region w.r.t to ‘dy’ as well. Here, we need to put values of ‘x’ from both the given equations and hence, by integrating them, we can get an area of the shaded region. Be clear with the formula $\int{\sqrt{{{a}^{2}}-{{x}^{2}}}}dx$ . one need to remember all these formulae with the kind of point C to point A by taking 0 difference of area of circle and given parabola with the x-axis. questions.Calculation is the important part of the question.