Question

Find the area of region, $\\{(x,y):{{y}^{2}}\le 4x,4{{x}^{2}}+4{{y}^{2}}\le a\\}$ using the method of integration.

Answer 1

First, see the region by making the graph in $xy$-plane and try to evaluate the limits of $x$ and $y$, such that one of the limits has constant value and then solve the double integration with respect to $x$ and $y$ .

Complete step by step answer:
In the question , we are given a region whose area we have to evaluate and we know that for evaluating the area of a region we evaluate double integration with respect to $x$ and $y$ .

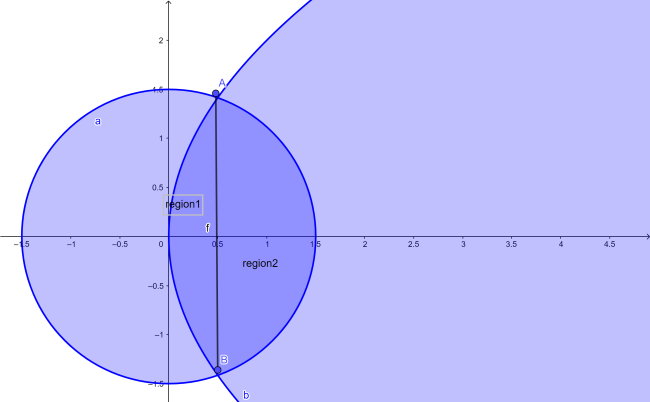
Hence,
Area of the region $\begin{aligned} & =\iint{dxdy} \\\ & \end{aligned}$
As we can see that the whole region cannot be evaluated simultaneously under a single curve as the 2 subregions have the area under 2 different curves, so we have to evaluate them separately.
$=\iint{{}}$region 1 $+\iint{{}}$ region2
Intersection point of the curves will be,
$\begin{aligned} & \dfrac{-4{{x}^{2}}+9}{4}=4x \\\ &\Rightarrow -4{{x}^{2}}+9=16x \\\ &\Rightarrow 4{{x}^{2}}+16x-9=0 \\\ &\Rightarrow x=\dfrac{1}{2} \end{aligned}$
Hence, for the first region $x$ has range from 0 to $\dfrac{1}{2}$
And in region 1 we have area under the parabola
, so $y$ will range from 0 to $2\sqrt{x}$
and for the second region $x$ will range from $\dfrac{1}{2}$ to $\dfrac{3}{2}$
and since in region 2 we have area under circle, $y$ will range from 0 to $\dfrac{1}{2}\sqrt{9-4{{x}^{2}}}$
By putting the limits, we get
[While solving this, we are going to get an integration of the form $\int{\sqrt{{{a}^{2}}-{{x}^{2}}}}$
Which is equal to $\dfrac{1}{2}x\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{1}{2}{{a}^{2}}{{\operatorname{Sin}}^{-1}}\dfrac{x}{a}$ , but the form in our question involves $2x$ instead of $x$ , so now we will use the same formula for $2x$ and divide the RHS of the formula by 2]

& =2\int\limits_{0}^{\dfrac{1}{2}}{\int\limits_{0}^{2\sqrt{x}}{dxdy+\dfrac{1}{2}\int\limits_{\dfrac{1}{2}}^{\dfrac{3}{2}}{\int\limits_{0}^{\dfrac{1}{2}\sqrt{9-4{{x}^{2}}}}{dxdy}}}} \\\ & =2\int\limits_{0}^{\dfrac{1}{2}}{2\sqrt{x}dx+}\dfrac{1}{2}\int\limits_{\dfrac{1}{2}}^{\dfrac{3}{2}}{\dfrac{1}{2}\sqrt{9-4{{x}^{2}}}dx} \\\ & =\left. 4\left[ \dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right]_{0}^{\dfrac{1}{2}}+\dfrac{1}{2}\left( \dfrac{1}{2}2x\sqrt{9-4{{x}^{2}}}+\dfrac{9}{2}{{\operatorname{Sin}}^{-1}}\left( \dfrac{2x}{3} \right) \right) \right|_{\dfrac{1}{2}}^{\dfrac{3}{2}} \\\ & =\dfrac{8}{3}\dfrac{1}{2\sqrt{2}}+\dfrac{9}{4}{{\operatorname{Sin}}^{-1}}1-\dfrac{1}{4}\sqrt{8}-\dfrac{9}{4}{{\operatorname{Sin}}^{-1}}\dfrac{1}{3} \\\ & =\dfrac{\sqrt{2}}{6}+\dfrac{9\pi }{8}-\dfrac{9}{4}{{\operatorname{Sin}}^{-1}}\dfrac{1}{3} \end{aligned}$$ **Note:** The possibility of mistake here is , sometimes we forget here that there are 2 separate regions , 2 separate regions under 2 different curves , so we have to evaluate them separately, taking the limits with respect to the area under that curve.