Question
Question: Find the area of quadrilateral ABCD. 
Solution
Hint:First look at the figure given and try to find out the name of shape. By using different properties you can eliminate some of the shapes and arrive at the conclusion of a particular shape. By using knowledge of geometry try to change the formula or area and use the formula of area and use the formula which is suitable for the given question.
Complete step-by-step answer:
The given quadrilateral
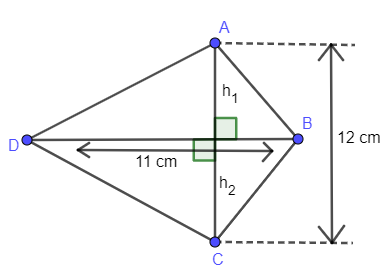
So, you can see the lengths of diagonals are different.
By above you can eliminate squares and rectangles.
You can see diagonals are bisecting. So, you can eliminate kites from this condition.
Now by observation, you can see diagonals are perpendicular to each other. So, we can confirm that it is rhombus by above conditions.
Now take diagonal DB, it is dividing the shape into 2 triangles with the same base BD.
As we know that diagonals bisects each other we say the height of both triangles is half the length of AC.
By above conditions we can say area of ABCD, is:
Area of ABCD = Area of ΔABD+ Area of ΔBCD
ΔABD=21×base×height
Above formula is well known from geometry
ΔABD=ΔBCD=21×11×6=33
Area of ABCD =2×33
=66 sq. cm
Note: Alternate method is to apply direct formula that area =21(d1d2) where d1,d2 are lengths of the diagonals i.e d1=12cm and d2=11cm by substituting in above formula we get required answer.Students should remember the formulas of area of triangle and quadrilateral to solve these types of questions.
