Question
Question: Find the area of pentagon\(PQRST\)in which \(QD \bot PR,RE \bot PS\)and \(TF \bot PS\)such that \(PR...
Find the area of pentagonPQRSTin which QD⊥PR,RE⊥PSand TF⊥PSsuch that PR=10cm, PS=12cm, QD=3cm, RE=7cmand TF=5cm.
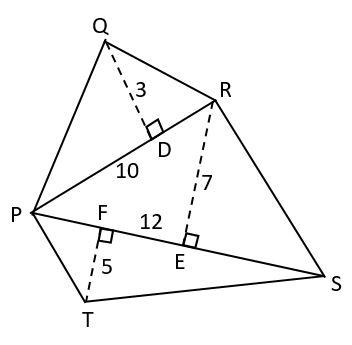
Solution
It is better to understand a pentagon is a five-sided polygon in geometry. In the given question, the sides of the pentagon are different so do not use the properties of a regular pentagon.
Complete step by step Solution:
From the given figure,
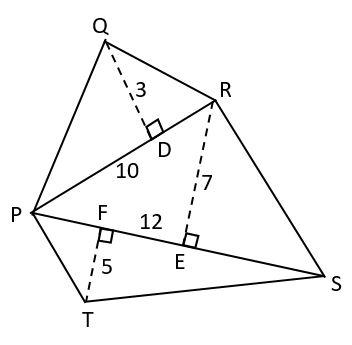
We can observe that the pentagon can be separated into three triangles namely, ΔPQR, ΔPRSand ΔPTS
If we find the areas of these three triangles, then the sum of areas of all three angles will give us the area of the given pentagon i.e.
ar(ΔPQR)+ar(ΔPRS)+ar(ΔPTS)=ar(PQRST) . . . (1)
We know that, for a triangle with base b and perpendicular h, the area of a triangle is
=21×b×h
In ΔPQR
It is given that QD⊥PR
Thus we can write
ar(ΔPQR)=21×PR×QD
Substituting the given values of PR and QD, we get
ar(ΔPQR)=21×10×3
⇒ar(ΔPQR)=15cm2 . . . (2)
In ΔPRS
It is given that RE⊥PS
Thus we can write
ar(ΔPRS)=21×RE×PS
Substituting the given values of RE and PS, we get
ar(ΔPRS)=21×7×12
⇒ar(ΔPRS)=42cm2 . . . (3)
InΔPTS
It is given that TF⊥PS
Thus we can write
ar(ΔPTS)=21×PS×TF
Substituting the given values of PS and TF, we get
ar(ΔPTS)=21×12×5
⇒ar(ΔPTS)=30cm2 . . . (4)
From equation (1)
ar(ΔPQR)+ar(ΔPRS)+ar(ΔPTS)=ar(PQRST)
Substituting the values of areas of respective triangles from equation (2), (3) and (4), we get
ar(PQRST)=15+42+30
⇒ar(PQRST)=87cm2
Hence, Area of pentagonPQRSTis 87cm2
Note: This question was made easy by giving all the required values. But it is not always necessary that you will be given all this information. In such cases, to solve the problems on any polygon, you need to know their properties. Like, sum of angles and properties of regular polygons.
