Question

Find the area lying above X-axis and included between the circle ${x^2} + {y^2} = 8x$ and inside the parabola ${y^2} = 4x.$

Answer 1

Hint : $\int\limits_a^b {f(x)dx}$ represents area under the curve $f(x)$ between the points $x = a$ and $x = b$ above X-axis

** Complete step-by-step answer** :
Since equation of circle with center $(h,k)$ and radius $r$ is given by equation,
${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$
We convert our equation to the above form to get the coordinates of the center of the circle and the radius of the circle.
We have
${x^2} + {y^2} = 8x$ . . . (1)
Rearranging it, we get
${x^2} - 8x + {y^2} = 0$
$\Rightarrow {x^2} - 2 \times 4 \times x + {y^2} = 0$
Add ${4^2}$ to both the sides
$\Rightarrow {x^2} - 2 \times 4 \times x + {4^2} + {y^2} = {4^2}$
$\Rightarrow {\left( {x - 4} \right)^2} + {y^2} = {4^2}$ $\left( {\because {{(a - b)}^2} = {a^2} + 2ab + {b^2}} \right)$ . . . (2)
So, circle has centers $\left( {4,0} \right)$ and radius $= 4$
Equation of parabola with vertex at the origin is given by
${y^2} = 4ax$
We have the equation of parabola as
${y^2} = 4x$ . . . (3)
Thus, here $a = 1$ and the parabola has vertex at the origin.
To find the point of intersection of parabola and circle, put the value of ${y^2}$ from equation (3) into equation (1)
Therefore, equation (1) becomes
${x^2} + 4x = 8x$
Re-arranging it, we get
${x^2} + 4x - 8x = 0$
$\Rightarrow {x^2} - 4x = 0$
$\Rightarrow x(x - 4) = 0$
$\Rightarrow x = 0$ or $x = 4$
Therefore, the parabola and the circle are intersecting at points $x = 0$ and $x = 4$
Now, using equation (2), equation (3) and the point of intersections, we can draw the graph as

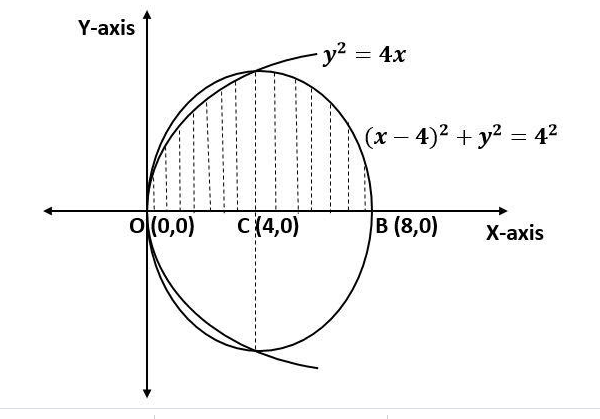
We need to find the area of the shaded region.
Now, we know that
$\int\limits_a^b {f(x)dx}$ represents area under the curve $f(x)$ between the points $x = a$ and $x = b$ above X-axis
The area in the shaded region is under two curves
${y^2} = 4x$ from $x = 0$ to $x = 4$
And
${\left( {x - 4} \right)^2} + {y^2} = {4^2}$ from $x = 4$ to $x = 8$
Let the required area in the shaded region is given by $A$
Then
$A = \int\limits_0^4 {{f_1}(x)dx} + \int\limits_4^8 {{f_2}(x)dx}$ . . . (1)
Where,
${f_1}(x) = y = \sqrt {4x}$
And
${f_2}(x) = y = \sqrt {{4^2} - {{\left( {x - 4} \right)}^2}}$
$\Rightarrow A = \int\limits_0^4 {\sqrt {4x} dx} + \int\limits_4^8 {\sqrt {{4^2} - {{\left( {x - 4} \right)}^2}} dx}$ . . . (4)
Let ${I_1} = \int\limits_0^4 {\sqrt {4x} dx}$
$\Rightarrow {I_1} = 2\int\limits_0^4 {\sqrt x dx}$ $\left( {\because \int {kf(x)dx = k\int {f(x)dx} } } \right)$
$\Rightarrow {I_1} = 2\int\limits_0^4 {{x^{\dfrac{1}{2}}}dx}$
$= 2\left[ {\dfrac{{{x^{\dfrac{1}{2} + 1}}}}{{\dfrac{1}{2} + 1}}} \right]_0^4$ $\left( {\because \int {{x^n}dx = \dfrac{{{x^{n + 1}}}}{{n + 1}}} + C} \right)$
$= 2\left[ {\dfrac{{{x^{\dfrac{3}{2}}}}}{{\dfrac{3}{2}}}} \right]_0^4$
Substituting the upper and lower limits and simplifying it, we get
$= \dfrac{4}{3}\left[ {{4^{\dfrac{3}{2}}} - 0} \right]$ $\left( {\because \left[ {F(x)} \right]_a^b = F(b) - F(a)} \right)$
$= \dfrac{4}{3} \times {2^3}$
$\Rightarrow {I_1} = \dfrac{{32}}{3}$ . . . (5)
Let ${I_2} = \int\limits_4^8 {\sqrt {{4^2} - {{\left( {x - 4} \right)}^2}} dx}$
We know that
$\int {\sqrt {{a^2} - {x^2}} dx = } \dfrac{x}{2}\sqrt {{a^2} - {x^2}} + \dfrac{{{a^2}}}{2}{\sin ^{ - 1}}\left( {\dfrac{x}{a}} \right) + C$
Using this formula, we can write
${I_2} = \left[ {\dfrac{{x - 4}}{2}\sqrt {{4^2} - {{\left( {x - 4} \right)}^2}} + \dfrac{{{4^2}}}{2}{{\sin }^{ - 1}}\left( {\dfrac{{x - 4}}{4}} \right)} \right]_4^8$
$\Rightarrow {I_2} = \left[ {\dfrac{{8 - 4}}{2}\sqrt {{4^2} - {{\left( {8 - 4} \right)}^2}} + \dfrac{{{4^2}}}{2}{{\sin }^{ - 1}}\left( {\dfrac{{8 - 4}}{4}} \right) - \left( {\dfrac{{4 - 4}}{2}\sqrt {{4^2} - {{\left( {4 - 4} \right)}^2}} + \dfrac{{{4^2}}}{2}{{\sin }^{ - 1}}\left( {\dfrac{{4 - 4}}{4}} \right)} \right)} \right]$
By simplifying it, we get
${I_2} = \dfrac{4}{2}\sqrt {{4^2} - {{\left( 4 \right)}^2}} + \dfrac{{{4^2}}}{2}{\sin ^{ - 1}}\left( {\dfrac{4}{4}} \right) - 0 + 0$ $\left( {\because {{\sin }^{ - 1}}(0) = 0} \right)$
$\Rightarrow {I_2} = \dfrac{{16}}{2}{\sin ^{ - 1}}(1)$
$\Rightarrow {I_2} = 8 \times \dfrac{\pi }{2}$ $\left( {\because {{\sin }^{ - 1}}(1) = \dfrac{\pi }{2}} \right)$
$\Rightarrow {I_2} = 4\pi$ . . . (6)
By substituting the values of ${I_1}$ and ${I_2}$ from equation (5) and (6) into equation (4), we get
$A = \dfrac{{32}}{3} + 4\pi$ sq. units
Therefore, the required area is, $\dfrac{{32}}{3} + 4\pi$ sq. units

Note : It is extremely important to note that $\int\limits_a^b {f(x)dx}$ gives the area under the curve $f(x)$ and above the X-axis. If the curve is under the X-axis then this integral will give a negative answer. But the area cannot be negative. Therefore, whenever the curve is under X-axis, we will write the above integral in mod. i.e. $\left| {\int\limits_a^b {f(x)dx} } \right|$