Question

Find the area in(sq. units) of the region bounded by the curve $y = f\left( x \right){\text{ and y}} = g\left( x \right)$ between the lines $2x = 1{\text{ and }}2x = \sqrt 3$ , when $f\left( x \right){\text{ and }}g\left( x \right)$ are given as:
f\left( x \right) = \left\\{ \begin{gathered} x,0 \leqslant x < \dfrac{1}{2} \\\ \dfrac{1}{2},x = \dfrac{1}{2} \\\ 1 - x,\dfrac{1}{2} < x \leqslant 1 \\\ \end{gathered} \right\\}{\text{ }} and
${\text{g}}\left( x \right) = {\left( {x - \dfrac{1}{2}} \right)^2},x \in R$
A. $\dfrac{1}{3} + \dfrac{{\sqrt 3 }}{4}$
B. $\dfrac{1}{2} - \dfrac{{\sqrt 3 }}{4}$
C. $\dfrac{1}{2} + \dfrac{{\sqrt 3 }}{4}$
D. $\dfrac{{\sqrt 3 }}{4} - \dfrac{1}{3}$

Answer 1

First, plot the graph of the given equations and make a rough sketch of the area to be founded.
Then find the limits within which curve is bounded i.e. x=a to x= b. In this question the limits are already given i.e. $x = \dfrac{1}{2}{\text{ }}$to ${\text{ }}x = \dfrac{{\sqrt 3 }}{2}$. These limits will become the limits for the integration.
The area bounded between two curves is given by:
$\int\limits_{x = a}^{x = b} {\left( {{y_2} - {y_1}} \right)dx}$
Where, $y_2$ represents the upper bounding curve and $y_1$ represents the lower bounding curve.

Complete step by step solution:
The given equations are:
$y = {\text{ }}x{\text{ }}$when ${\text{0}} \leqslant x < \dfrac{1}{2}{\text{ }} - - - (i)$
${\text{y = }}\dfrac{1}{2}$ when $x = \dfrac{1}{2}{\text{ - - - - - - - - - - - - - - - - - - - - - - - - - - }}\left( {ii} \right)$
${\text{y = }}1 - x$ when $\dfrac{1}{2} < x \leqslant 1{\text{ - - - - - - - - - - - - - - - - - - }}\left( {iii} \right)$
And ${\text{ }}y = {\left( {x - \dfrac{1}{2}} \right)^2}{\text{ - - - - - - - - - - - - - - - - - - - - - - - - - - - - - }}\left( {iv} \right)$
Equation (i) represents a straight line passing through origin, and making an angle of $45^\circ$ with x-axis,
between $x = 0$ and $x = \dfrac{1}{2}$.
Equation (ii) represents the point $\left( {\dfrac{1}{2},\dfrac{1}{2}} \right)$.
Equation (iii) represents a straight line.
Putting $y = 0$ and $x = 0$ respectively in equation (iii), we obtain:
$x = 1$ and $y = 1$ respectively.
So, the straight line passes through points $\left( {1,0} \right)$and $\left( {0,1} \right)$, but required portion is only between $x = \dfrac{1}{2}$and $x = 1$.
Equation (iv) represents a parabola having vertex at $\left( {\dfrac{1}{2},0} \right)$ , and axis along the positive y-axis.
The area bounded by these curves between lines $2x = 1$and $2x = \sqrt 3$ is shown below.

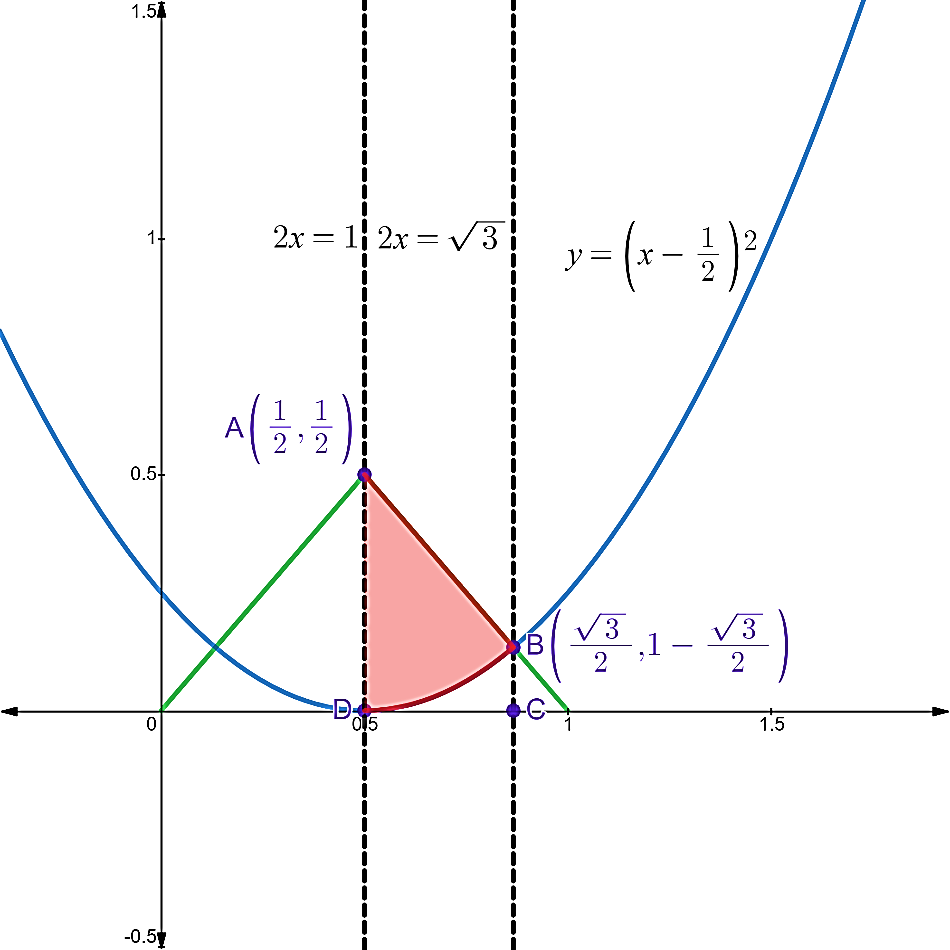
In order to find the point of intersection of line and parabola we solve the equations (iii) and (iv) simultaneously.
From (iii) we get, $y = 1 - x$
Putting this value of y in (iv), we get:
$1 - x = {\left( {x - \dfrac{1}{2}} \right)^2}$
$1 - x = {\left( {\dfrac{{2x - 1}}{2}} \right)^2}$
$1 - x = \dfrac{{{{\left( {2x - 1} \right)}^2}}}{4}$
Using the identity ${(a - b)^2} = {a^2} + {b^2} - 2ab$, we have
$\Rightarrow 1 - x = \dfrac{{4{x^2} - 4x + 1}}{4}$
Cross multiplying we have,
$\Rightarrow 4 - 4x = 4{x^2} - 4x + 1$
Cancelling ‘4x’ we have,
$\Rightarrow 4{x^2} = 3$
Divide by 4 on both sides of the equation
$\Rightarrow {x^2} = \dfrac{3}{4}$
Taking square root on both side we have,
$\Rightarrow x = \dfrac{{\sqrt 3 }}{2}$
Putting $x = \dfrac{{\sqrt 3 }}{2}$ , in equation (iii)
$\Rightarrow y = 1 - \dfrac{{\sqrt 3 }}{2}$
There intersection point is:
$B\left( {\dfrac{{\sqrt 3 }}{2},1 - \dfrac{{\sqrt 3 }}{2}} \right)$
Now, we have to find the area of the bounded region ABDA.
Area of region ABDA:
= area under line AB – area under the parabola between $x = \dfrac{1}{2}$ and $x = \dfrac{{\sqrt 3 }}{2}$
Area bounded between two curves is given by:
$\int\limits_{{x_1}}^{{x_2}} {\left( {{y_2} - {y_1}} \right)dx}$
Where, y2 represents the upper bounding curve and y1 represents the lower bounding curve.
Here, upper bounding curve is:
${y_2} = 1 - x$
and lower bounding curve is:
${y_1} = {\left( {x - \dfrac{1}{2}} \right)^2}$
Area of region ABDA after substituting the values we have,
$= \int\limits_{\dfrac{1}{2}}^{\dfrac{{\sqrt 3 }}{2}} {\left( {\left( {1 - x} \right) - {{\left( {x - \dfrac{1}{2}} \right)}^2}} \right)dx}$
Using the identity ${(a - b)^2} = {a^2} + {b^2} - 2ab$, we have
$= \int\limits_{\dfrac{1}{2}}^{\dfrac{{\sqrt 3 }}{2}} {\left( {1 - x - {x^2} + x - \dfrac{1}{4}} \right)dx}$
Cancelling ‘x’ we get:
$= \int\limits_{\dfrac{1}{2}}^{\dfrac{{\sqrt 3 }}{2}} {\left( {\dfrac{3}{4} - {x^2}} \right)dx}$
integrating we have,
$= \left[ {\dfrac{{3x}}{4} - \dfrac{{{x^3}}}{3}} \right]_{\dfrac{1}{2}}^{\dfrac{{\sqrt 3 }}{2}}$
Applying upper and lower bond we have,
$= \left[ {\dfrac{{3\sqrt 3 }}{8} - \dfrac{{3\sqrt 3 }}{{24}}} \right] - \left[ {\dfrac{3}{8} - \dfrac{1}{{24}}} \right]$
$\Rightarrow \left[ {\dfrac{{9\sqrt 3 - 3\sqrt 3 }}{{24}}} \right] - \left[ {\dfrac{{9 - 1}}{{24}}} \right]$
$\Rightarrow \left[ {\dfrac{{3\sqrt 3 - \sqrt 3 }}{8}} \right] - \left[ {\dfrac{7}{{24}}} \right]$
$\Rightarrow \left[ {\dfrac{{\sqrt 3 (3 - 1)}}{8}} \right] - \left[ {\dfrac{7}{{24}}} \right]$
$\Rightarrow \left[ {\dfrac{{2\sqrt 3 }}{8}} \right] - \left[ {\dfrac{7}{{24}}} \right]$
$\Rightarrow \dfrac{{\sqrt 3 }}{4} - \dfrac{1}{3}$

So, the correct answer is Option D.

Note: If the functions give are in the form of $x = f\left( y \right)$ and $x = g\left( y \right)$ and bounded by lines $y = c$ and $y = d$ then area Is given by formula:
$= \int\limits_c^d {\left( {f(y) - g\left( y \right)} \right)dy}$ where $f\left( y \right) > g\left( y \right)$.