Question

Find the area enclosed by the curve $x=3\cos t$, $y=2\sin t$?

Answer 1

For the given question we are given a parametric equation and asked to find the area enclosed by the graph. By converting given parametric equations to x and y forms we can see that they will be converted into an eclipse graph as we know that the area of any eclipse graph is 4 times of the symmetrical part. Therefore we can find the area of the graph.

Complete step-by-step answer:
For the given problem we are given to find the area enclosed by the curve $x=3\cos t$ and $y=2\sin t$.
Let us consider given 2 equations as equation (1) and equation (2).
$x=3\cos t....................\left( 1 \right)$
$y=2\sin t...................\left( 2 \right)$
As we know the identity ${{\cos }^{2}}t+{{\sin }^{2}}t=1$. So let us consider the identity as (I1).
${{\cos }^{2}}t+{{\sin }^{2}}t=1...........\left( I1 \right)$
Let us find the value of $\cos t$ and $\sin t$ from equation (2) and equation (1) respectively.
From equation (1) and equation (2), we get
$\dfrac{x}{3}=\cos t$ and $\dfrac{y}{2}=\sin t$.
Let us substitute the above values in identity (I1), we get
$\Rightarrow {{\left( \dfrac{x}{3} \right)}^{2}}+{{\left( \dfrac{y}{2} \right)}^{2}}=1$
Let us consider the above equation as equation (3).
$\Rightarrow {{\left( \dfrac{x}{3} \right)}^{2}}+{{\left( \dfrac{y}{2} \right)}^{2}}=1.......................\left( 3 \right)$
Let us plot the graph for the above equation

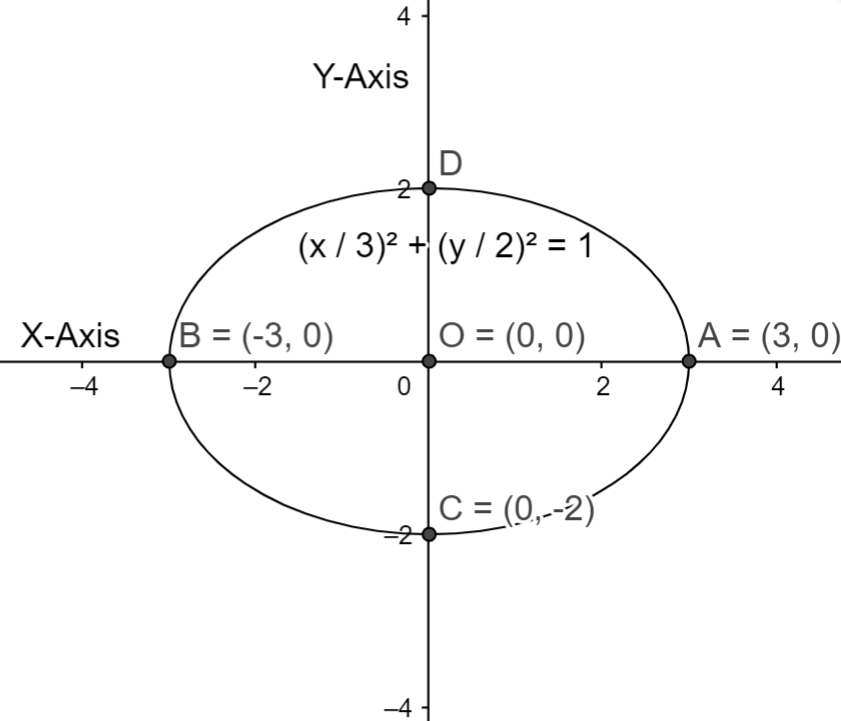
As we know the equation of eclipse is in the form $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. So, as we know that the graph is symmetrically partitioned by 4 parts. Therefore, by finding the one part we can find the total area of the graph.
$\Rightarrow \text{Area=4}\text{.Area of OAB}$
$=4\int\limits_{0}^{3}{ydx}$
Let us consider the above equation as equation (4).
$A=4\int\limits_{0}^{3}{ydx}...................\left( 4 \right)$
Therefore, from the equation (1) we get
$\Rightarrow y=\left( \dfrac{2}{3}\sqrt{\left( 9-{{x}^{2}} \right)} \right)$
Let us substitute the above value in equation (4) we get,
$\Rightarrow A=4\int\limits_{0}^{3}{\left( \dfrac{2}{3}\sqrt{\left( 9-{{x}^{2}} \right)} \right)dx}$
$\Rightarrow A=\dfrac{8}{3}\int\limits_{0}^{3}{\left( \sqrt{\left( {{3}^{2}}-{{x}^{2}} \right)} \right)dx}$
Let us consider above equation as equation (5).
$\Rightarrow A=\dfrac{8}{3}\int\limits_{0}^{3}{\left( \sqrt{\left( {{3}^{2}}-{{x}^{2}} \right)} \right)dx}.........\left( 5 \right)$
By the formula $\int{{{a}^{2}}-{{x}^{2}}dx=\left| \dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a} \right|}$
By applying the formula to the equation (5), we get
$\Rightarrow A=\dfrac{8}{3}\left| \dfrac{x}{2}\sqrt{{{3}^{2}}-{{x}^{2}}}+\dfrac{9}{2}{{\sin }^{-1}}\dfrac{x}{3} \right|_{0}^{3}$
$\Rightarrow A=\dfrac{8}{3}\left| \dfrac{9}{2}{{\sin }^{-1}}\left( \sin \dfrac{\pi }{2} \right) \right|$
$\Rightarrow A=6\pi squnits$
Therefore, the area of the given graph is $6\pi squints$.

Note: While doing this problem we have to remember a point that we have to convert the given parametric equation to the geometric equation to get the graph. We should be aware of all integration formulas to solve this question