Solveeit Logo
Login

Question

Question: Find the area enclosed between the parabola \(4y = 3{x^2}\) and the straight line \(3x - 2y + 12 = 0...

Find the area enclosed between the parabola 4y=3x24y = 3{x^2} and the straight line 3x−2y+12=03x - 2y + 12 = 0

Explanation

Solution

Hint-In order to solve this question firstly, we have to find the area enclosed between the parabola using integration. Then we will get our desired answer. There is need to aware about some basic integration methods and formulas

Complete step-by-step solution -


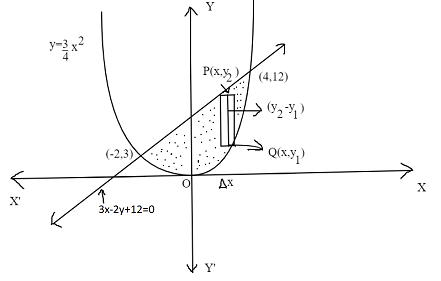
The area under a curve between two points can be found by doing a definite integral between the two points. To find the area under the curve y=f(x) between x = a and x = b, integrate y=f(x) between the limits of an and b. Areas under the x-axis will come out negative and areas above the x-axis will be positive.

The given equations are –
y = 3x24y{\text{ = }}\dfrac{{3{x^2}}}{4} ……… (1)
And, 3x−2y+12=03x - 2y + 12 = 0 …….. (2)
Solving equations (1) and (2) we get
y=3x+122y = \dfrac{{3x + 12}}{2}
Now, by using the quadratic equation to solve the equation of parabola,
4y=3x2 4(3x+122)=3x2 2(3x+12)=3x2 3x2−6x−24=0 3(x2−2x−8)=0  4y = 3{x^2} \\\ 4\left( {\dfrac{{3x + 12}}{2}} \right) = 3{x^2} \\\ 2\left( {3x + 12} \right) = 3{x^2} \\\ 3{x^2} - 6x - 24 = 0 \\\ 3\left( {{x^2} - 2x - 8} \right) = 0 \\\
x2−2x−8=0 x2−4x+2x−8=0 x(x−4)+2(x−4)=0 (x+2)(x−4)=0  {x^2} - 2x - 8 = 0 \\\ {x^2} - 4x + 2x - 8 = 0 \\\ x\left( {x - 4} \right) + 2\left( {x - 4} \right) = 0 \\\ \left( {x + 2} \right)\left( {x - 4} \right) = 0 \\\
For, x=4, y=3×4+122=12 ⇒y=12  x = 4, \\\ y = \dfrac{{3 \times 4 + 12}}{2} = 12 \\\ \Rightarrow y = 12 \\\
For x=−2, y=3×(−2)+122=12 ⇒y=3  x = - 2, \\\ y = \dfrac{{3 \times ( - 2) + 12}}{2} = 12 \\\ \Rightarrow y = 3 \\\
∴\therefore intersection points are (-2, 3) & (4, 12)
Hence, the required area will be a shaded region.
A=∫−24(3x−122 - 34x2)dx ⇒A=[34x2+6x−x34]−24 =(12+24−16)−(3−12+2) =20+7 ⇒A=27sq. units.  A = \int\limits_{ - 2}^4 {\left( {\dfrac{{3x - 12}}{2}{\text{ - }}\dfrac{3}{4}{x^2}} \right)} dx \\\ \Rightarrow A = \left[ {\dfrac{3}{4}{x^2} + 6x - \dfrac{{{x^3}}}{4}} \right]_{ - 2}^4 \\\ = \left( {12 + 24 - 16} \right) - \left( {3 - 12 + 2} \right) \\\ = 20 + 7 \\\ \Rightarrow A = 27sq.{\text{ units}}{\text{.}} \\\
Required area= 27 units.

Note- Whenever we come up with this type of problem, one should know that we have to use integration to find the area enclosed between a parabola and a straight line and quadratic equations to find the points of intersection. By using this approach, we will get our answer.