Question

Find the area cut off from the parabola $4y=3{{x}^{2}}$ by the straight line $2y=3x+12$.
(a) 25 sq. units
(b) 27 sq. units
(c) 36 sq. units
(d) 16 sq. units

Answer 1

In this question, first draw the graph according to the conditions given, determine the points both the graphs of the parabola and straight line intersect, note down those points. Find the area by using integration with values of $x$as its limits and by subtracting the parabola equation from the straight-line equation inside the integral. Solve the integral and find the area of the enclosed part.

Complete step-by-step solution:
Let us first draw the parabola in the graph to check the figure,
We need to know, the points to plot on the graph for the parabola, let us find the points for the parabola $4y=3{{x}^{2}}$.
Divide the above expression by 4, we get
$y=\dfrac{3}{4}{{x}^{2}}$
Let us take the values of $x$ as -3, -2, -1, 0, 1, 2, 3 and find the values of $y$ by substituting in the above expression.

$x$	$y$
-2	3
-1	0.75
0	0
1	0.75
2	3

Now, let us plot these points and draw the curve through all these points which will give us the parabola.

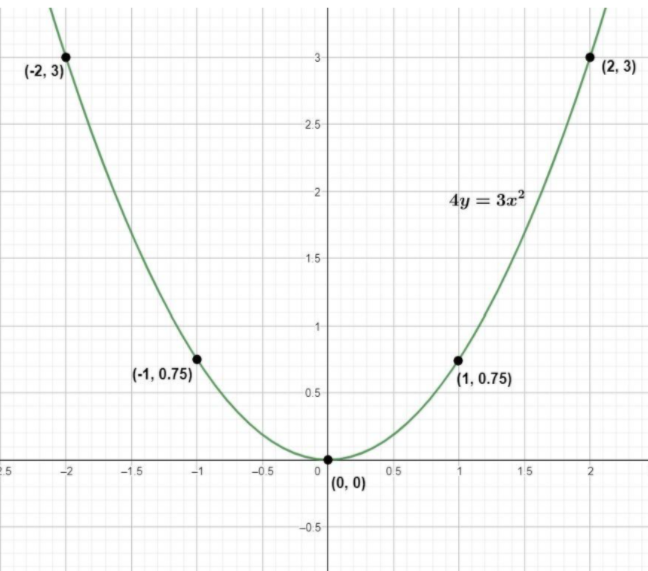
Now, let us also plot the straight line by substituting the values -2, 2 in the equation $2y=3x+12$ and find the value of $y=\dfrac{3x+12}{2}4$

$x$	$y$
-2	3
2	9

Now, let us plot the points of the straight line and draw the straight line.

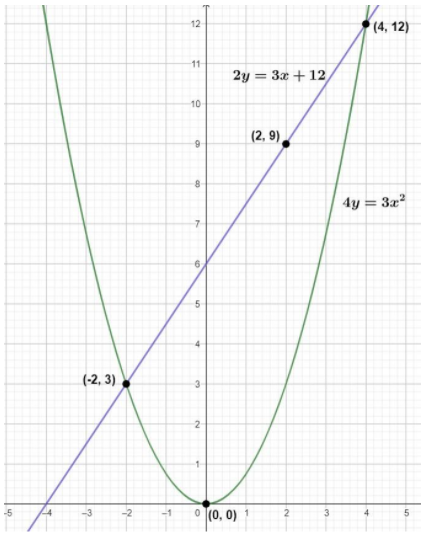
Here, we extended the line until it cuts the parabola on the point (4, 12)
Now, we need to find the area below the straight line and above the parabola curve, which is an enclosed space.
From the final graph, if we can see the straight line cuts the parabola at (-2, 3) and (4, 12).
Now, to find the area of the enclosed part we need to subtract the curve from the straight line. We will use definite integral to find the area
We know,
Equation of parabola in terms of $x$.

& 4y=3{{x}^{2}} \\\ & {{y}_{1}}=\dfrac{3}{4}{{x}^{2}} \end{aligned}$$ Equation of the straight line in terms of $x$. $\begin{aligned} & 2y=3x+12 \\\ & {{y}_{2}}=\dfrac{3x+12}{2} \end{aligned}$ We know from the graph, the limits of $x$is -2 and 4. Therefore, by integrating with respect to $x$,The area of the enclosed part = $\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{ydx}$ $\begin{aligned} & \text{A = }\int\limits_{-2}^{4}{\left( {{y}_{2}}-{{y}_{1}} \right)}\,dx \\\ & =\,\int\limits_{-2}^{4}{\left( \dfrac{3x+12}{2}-\dfrac{3}{4}{{x}^{2}} \right)}\,dx \\\ & =\int\limits_{-2}^{4}{\left( \dfrac{3}{2}x+6-\dfrac{3}{4}{{x}^{2}} \right)}\,dx \end{aligned}$ Solve the integrals according to the formulas required and find the area. $\begin{aligned} & \text{A = }\left[ \dfrac{3{{x}^{2}}}{4}+6x-\dfrac{3{{x}^{3}}}{12} \right]_{-2}^{4} \\\ & =\left[ \dfrac{3{{\left( 4 \right)}^{2}}}{4}+6\left( 4 \right)-\dfrac{3{{\left( 4 \right)}^{3}}}{4\times 3} \right]-\left[ \dfrac{3{{\left( -2 \right)}^{2}}}{4}+6\left( -2 \right)-\dfrac{3{{\left( -2 \right)}^{3}}}{4\times 3} \right] \\\ & =\left[ 12+24-16 \right]-\left[ 3-12+2 \right] \\\ & =\left[ 20 \right]-\left[ -7 \right] \\\ & =20+7 \\\ & =27 \end{aligned}$ Hence, the cut off area from the parabola by the straight line is 27 sq. units. **Note:** Here, you can also find the values of $x$ without drawing the graph, by equating both the equations and finding the value of $x$ and later following the similar steps to find the area. Also, remember to input the units after the result in order to avoid the deduction of marks. Here we have written the intersection points of line and parabola by drawing the graph, we can find these points by solving the equations algebraically.