Question

Find the area common to the circles $r=a\sqrt{2}$ and $r=2a\cos \theta$.

Answer 1

We solve this problem by first finding the equation of the given circles in cartesian form. Then we find the point of intersection of the circles and find the area of the circles between those obtained interval to find the area of the common region using the formula for area, $\int\limits_{a}^{b}{f\left( x \right)dx}$. Then we find the values of integral using the formula $\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx=}\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{a} \right)$. Then we double the obtained value to find the total area.

Complete step by step answer:
Given an equation of circles are $r=a\sqrt{2}$ and $r=2a\cos \theta$.
Let us find the equation of the first circle $r=a\sqrt{2}$.
As the radius is $r=a\sqrt{2}$, we get the equation of circle as
$\begin{aligned} & \Rightarrow {{x}^{2}}+{{y}^{2}}={{\left( \sqrt{2}a \right)}^{2}} \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}=2{{a}^{2}} \\\ \end{aligned}$
Now, let us find the equation of the second circle $r=2a\cos \theta$.
We can write the points on the circle as $x=r\cos \theta$ and $y=r\sin \theta$.
$x=r\cos \theta \Rightarrow \cos \theta =\dfrac{x}{r}$
Now let us substitute it in the value of r. Then we get,
$\begin{aligned} & \Rightarrow r=2a\cos \theta \dfrac{x}{r} \\\ & \Rightarrow r=2a\dfrac{x}{r} \\\ & \Rightarrow {{r}^{2}}=2ax \\\ \end{aligned}$
So, the equation of the second circle is
$\begin{aligned} & \Rightarrow {{x}^{2}}+{{y}^{2}}={{r}^{2}} \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}=2ax \\\ & \Rightarrow {{x}^{2}}-2ax+{{y}^{2}}=0 \\\ & \Rightarrow {{x}^{2}}-2ax+{{a}^{2}}+{{y}^{2}}={{a}^{2}} \\\ & \Rightarrow {{\left( x-a \right)}^{2}}+{{y}^{2}}={{a}^{2}} \\\ \end{aligned}$
Now let us find the point of intersection of the two curves. So, let us subtract the equation of second circle from the first. Then we get,
$\begin{aligned} & \Rightarrow \left( {{\left( x-a \right)}^{2}}+{{y}^{2}} \right)-\left( {{x}^{2}}+{{y}^{2}} \right)={{a}^{2}}-2{{a}^{2}} \\\ & \Rightarrow {{\left( x-a \right)}^{2}}-{{x}^{2}}=-{{a}^{2}} \\\ & \Rightarrow {{x}^{2}}-2ax+{{a}^{2}}-{{x}^{2}}=-{{a}^{2}} \\\ & \Rightarrow -2ax+{{a}^{2}}=-{{a}^{2}} \\\ & \Rightarrow 2ax=2{{a}^{2}} \\\ & \Rightarrow x=a \\\ \end{aligned}$
Now, let us plot the graph for the given two circles.

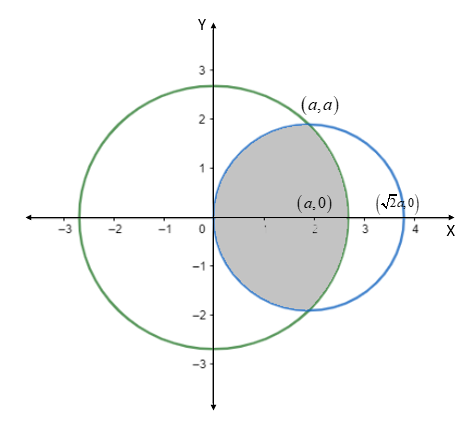
So, from the above figure we can see that the area we need to find is the sum of area of region between x=0 and $x=a$ of the second circle and the area between $x=a$ and $x=\sqrt{2}a$ of the first circle.
Now, let us consider the formula for area of region bounded by function $f\left( x \right)$ and x-axis,
$\int\limits_{a}^{b}{f\left( x \right)dx}$
Area of region between x=0 and $x=a$ of the second circle is
$\int\limits_{0}^{a}{\sqrt{{{a}^{2}}-{{\left( x-a \right)}^{2}}}dx}$
Now let us use the formula for $\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx=}\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{a} \right)$.
Then by applying the above formula we get,
$\Rightarrow \int\limits_{0}^{a}{\sqrt{{{a}^{2}}-{{\left( x-a \right)}^{2}}}dx}=\left[ \dfrac{\left( x-a \right)}{2}\sqrt{{{a}^{2}}-{{\left( x-a \right)}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x-a}{a} \right) \right]_{0}^{a}$
Substituting the values x=0 and x=a in it we get,

& \Rightarrow \left[ \dfrac{\left( a-a \right)}{2}\sqrt{{{a}^{2}}-{{\left( a-a \right)}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{a-a}{a} \right) \right]-\left[ \dfrac{\left( 0-a \right)}{2}\sqrt{{{a}^{2}}-{{\left( 0-a \right)}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{0-a}{a} \right) \right] \\\ & \Rightarrow \left[ \dfrac{0}{2}\sqrt{{{a}^{2}}-{{\left( 0 \right)}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{0}{a} \right) \right]-\left[ -\dfrac{a}{2}\sqrt{{{a}^{2}}-{{a}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{-a}{a} \right) \right] \\\ & \Rightarrow \left[ 0 \right]-\left[ -\dfrac{a}{2}\left( 0 \right)+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( -1 \right) \right] \\\ \end{aligned}$$ Simplifying it we get, $\begin{aligned} & \Rightarrow -\left[ 0+\dfrac{{{a}^{2}}}{2}\left( -\dfrac{\pi }{2} \right) \right] \\\ & \Rightarrow -\left[ -\dfrac{\pi {{a}^{2}}}{4} \right] \\\ & \Rightarrow \dfrac{\pi {{a}^{2}}}{4} \\\ \end{aligned}$ The area between $x=a$ and $x=\sqrt{2}a$ of the first circle is $\int\limits_{a}^{\sqrt{2}a}{\sqrt{2{{a}^{2}}-{{x}^{2}}}dx}$ By using the formula $\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx=}\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{a} \right)$ and applying it, we get $$\Rightarrow \int\limits_{a}^{\sqrt{2}a}{\sqrt{2{{a}^{2}}-{{x}^{2}}}dx}=\left[ \dfrac{x}{2}\sqrt{2{{a}^{2}}-{{x}^{2}}}+\dfrac{2{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{\sqrt{2}a} \right) \right]_{a}^{\sqrt{2}a}$$ Substituting the values $x=\sqrt{2}a$ and $x=a$ in it we get, $$\begin{aligned} & \Rightarrow \left[ \dfrac{\sqrt{2}a}{2}\sqrt{2{{a}^{2}}-2{{a}^{2}}}+{{a}^{2}}{{\sin }^{-1}}\left( \dfrac{\sqrt{2}a}{\sqrt{2}a} \right) \right]-\left[ \dfrac{a}{2}\sqrt{2{{a}^{2}}-{{a}^{2}}}+{{a}^{2}}{{\sin }^{-1}}\left( \dfrac{a}{\sqrt{2}a} \right) \right] \\\ & \Rightarrow \left[ \dfrac{\sqrt{2}a}{2}\left( 0 \right)+{{a}^{2}}{{\sin }^{-1}}\left( 1 \right) \right]-\left[ \dfrac{1}{2}\sqrt{{{a}^{2}}}+{{a}^{2}}{{\sin }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right) \right] \\\ & \Rightarrow \left[ 0+{{a}^{2}}\left( \dfrac{\pi }{2} \right) \right]-\left[ \dfrac{1}{2}a+{{a}^{2}}\left( \dfrac{\pi }{4} \right) \right] \\\ & \Rightarrow \left[ \dfrac{\pi {{a}^{2}}}{2} \right]-\left[ \dfrac{a}{2}+\dfrac{\pi {{a}^{2}}}{4} \right] \\\ & \Rightarrow \dfrac{\pi {{a}^{2}}}{4}-\dfrac{a}{2} \\\ \end{aligned}$$ So, by adding them, we get the area common to the both curves above x-axis. $\begin{aligned} & \Rightarrow \dfrac{\pi {{a}^{2}}}{4}+\dfrac{\pi {{a}^{2}}}{4}-\dfrac{a}{2} \\\ & \Rightarrow \dfrac{\pi {{a}^{2}}}{2}-\dfrac{a}{2} \\\ \end{aligned}$ As we need the area of region both above and below the x-axis and as the region is symmetrical, let us multiply the obtained area with 2, then we get, $\begin{aligned} & \Rightarrow 2\times \left( \dfrac{\pi {{a}^{2}}}{2}-\dfrac{a}{2} \right) \\\ & \Rightarrow \pi {{a}^{2}}-a \\\ \end{aligned}$ **Hence the answer is $\pi {{a}^{2}}-a$.** **Note:** The common mistake one does while solving this problem is one might not multiply the obtained answer after integrating with 2 and write the answer as $\dfrac{\pi {{a}^{2}}}{2}-\dfrac{a}{2}$. But we need to remember that the answer we got by integrating the curves is only the area of the region above the x-axis. So, we need to multiply the answer with 2.