Question

Find the area bounded by $y = x + 2,\,y = 2 - x$ and x-axis is (in square units):
a) 1
b) 2
c) 4
d) 6
e) 8

Answer 1

Hint: In this question, first plot the graph by finding out the points passing through the line given. This will give us a clear picture of what we have to find out. Here we have to calculate the area of the triangle. So, use this concept to reach the solution of the question.

Complete step-by-step answer:
Consider first linear equation given,
$y = x + 2$
Now we need to find out two coordinates which pass through this equation of line. So to find out two coordinates,
Firstly put $x = 0$ in the equation (1), we get,
$\Rightarrow y = 0 + 2$
$\Rightarrow y = 2$
Let us name the first coordinate as $A(x,y)$. By substituting $x$ and its corresponding $y$ value in $A(x,y)$ we get $A(0,2)$.
Similarly, we will find out the second coordinate of the same equation of line,
Now, we put $y = 0$ In equation (1), we get
$\Rightarrow 0 = x + 2$
By shifting +2 on LHS,
$\Rightarrow x = - 2$
Let us name this point as $B(x,y){\kern 1pt}$. By substituting $x$ and its corresponding $y$ value in $B(x,y){\kern 1pt}$ we get $B( - 2,0)$
Let us plot A and B co-ordinates on the graph of one-unit each on x-axis and y-axis and also draw a line joining A and B co-ordinate.

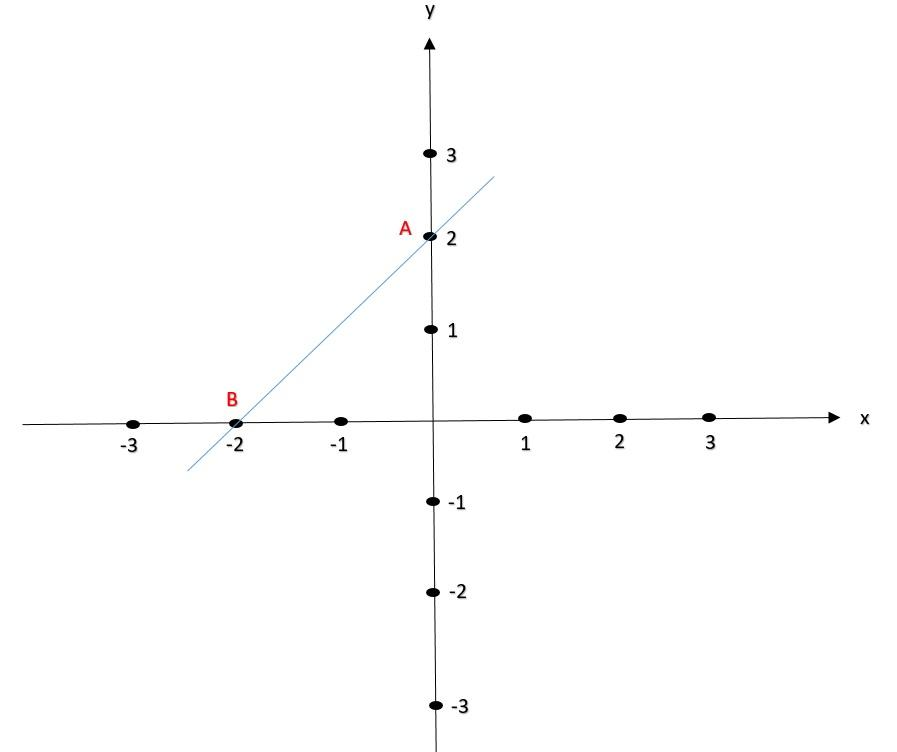
Fig (1)
Now, consider second linear equation given,
$y = 2 - x$
Let us find out two coordinates which pass through this equation of line.
Put $x = 0$ in equation (2), we get,
$\Rightarrow y = 2 - 0{\kern 1pt} {\kern 1pt}$
$\Rightarrow y = 2$
We get $(0,2)$
We have already named $(0,2)$ as A. So, one of the coordinate is $A(0,2)$
Now, put $y = 0$ in equation (2) to find out second coordinate,
$\Rightarrow 0 = x - 2$
Shifting -2 onto LHS we get,
$\Rightarrow x = 2$
Thus the second coordinate, say C is $C(2,0)$
Now, let us plot A and C points on the previous graph and draw a line by joining A and C.

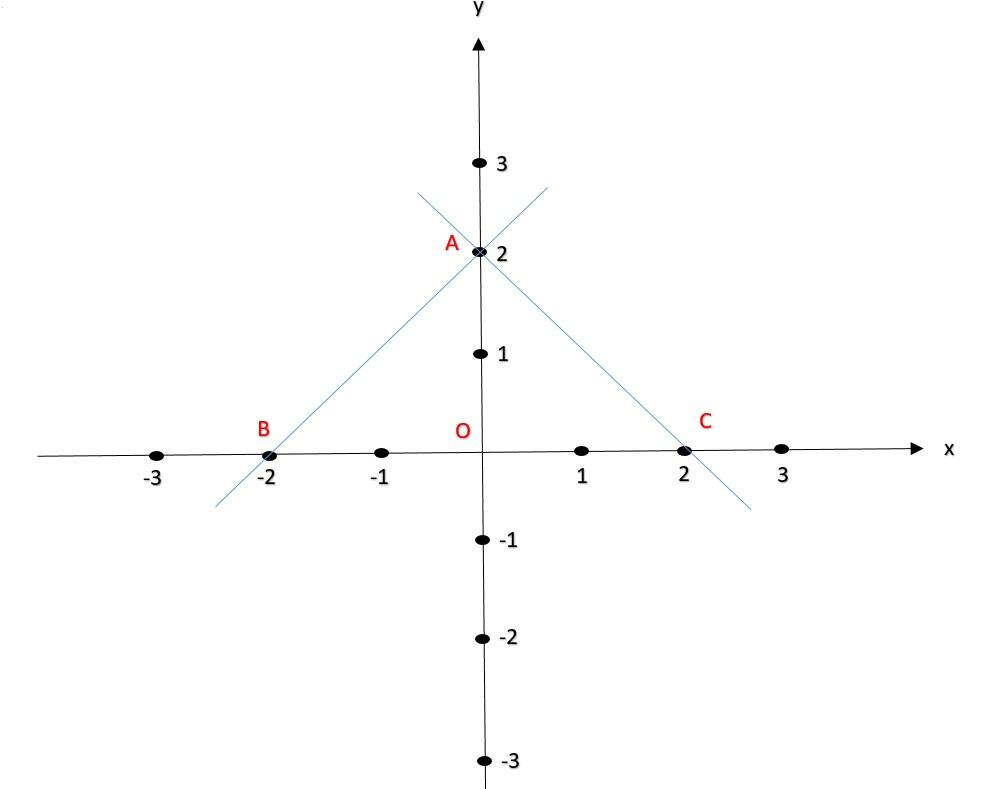
Fig (2)
Now, we need to find out the area bounded with these two linear equations i.e., (1) and (2) and x-axis, which is shown below (shaded region).

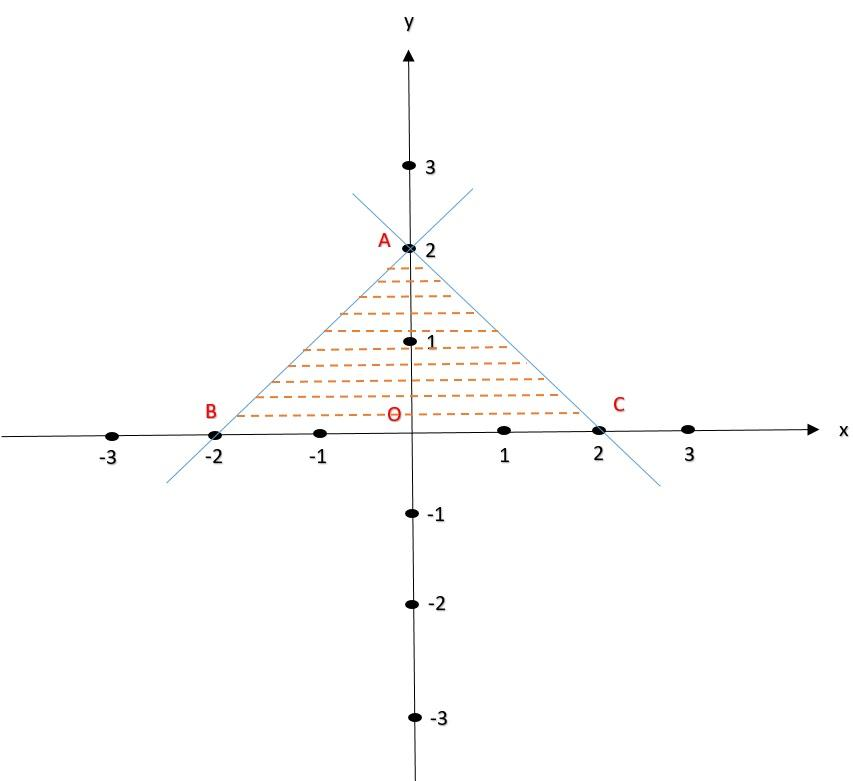
Fig (3)
The shaded region has two triangles $\Delta AOB{\kern 1pt}$ and $\Delta AOC$
Let us find out area of $\Delta AOB{\kern 1pt}$
We know that area of triangle is given by
Area of triangle = $\dfrac{1}{2} \times base \times height$
For $\Delta AOB{\kern 1pt}$, base is OB which is of 2 units and height is AO which is of 2 units.
Now, substitute base and height of $\Delta AOB{\kern 1pt}$ in equation (3).
$\Rightarrow$ Area of $\Delta AOB = \dfrac{1}{2} \times 2 \times 2$
$\Rightarrow$ Area of $\Delta AOB = 2{\rm{ sq}}{\rm{. units}}$
In the graph if we observe, the two triangles $\Delta AOB{\kern 1pt}$ and $\Delta AOC$ are symmetrical. Thus, the area is the same for both the triangles.
i.e.,
Area of $\Delta AOB$ = Area of $\Delta AOC = 2{\rm{ sq}}{\rm{. units}}$
Now, we will find area of $\Delta ABC$, by adding area of $\Delta AOB{\kern 1pt}$ and $\Delta AOC$,
Area of $\Delta ABC$ = Area of $\Delta AOB$ + Area of $\Delta AOC{\kern 1pt}$
$\Rightarrow$ Area of $\Delta ABC = 2 + 2$
$\Rightarrow$ Area of $\Delta ABC = 4{\rm{ sq}}{\rm{. units}}$
$\therefore$ The area bounded by given linear equation is $4{\rm{ sq}}{\rm{. units}}$
Option (c) is the correct answer.

Note: Whenever we face such type of questions first draw the pictorial representation of the given problem and then apply the formula of area of triangle as mentioned above. Substitute the values in the formula and simplify. we will get the required area bounded.