Question
Question: Find the area bounded by x = 1/2, x = 2, y = log<sub>e</sub> x and y = 2<sup>x</sup>-...
Find the area bounded by x = 1/2, x = 2, y = loge x and y = 2x-
A
log24−2+ 25log 2 + 23
B
log24−2– 25log 2 + 23
C
log24+2– 25log 2 + 23
D
None
Answer
log24−2– 25log 2 + 23
Explanation
Solution
Given curves are
y = log x ... (i)
y = 2x ... (ii)
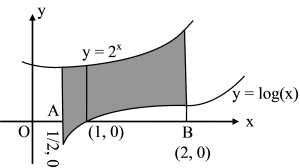
So, the required area
=  = ∫1/22(2x−logx)dx
= ∫1/22(2x−logx)dx
= 
= log24−2−(2log2−2)+(21log21−21)
= log24−2 – 25log 2 + 23.
