Question

Find the area bounded by the lines $x+2y=2$, $y-x=1$ and $2x+y=7$?

Answer 1

We start solving the problems by finding the intersection points of the three lines. We then draw the figure representing the lines and their intersection points. We then find the area of the triangle formed using the fact that the area of the triangle $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ is $A=\dfrac{1}{2}\left| \begin{matrix} {{x}_{1}}-{{x}_{2}} & {{x}_{1}}-{{x}_{3}} \\\ {{y}_{1}}-{{y}_{2}} & {{y}_{1}}-{{y}_{3}} \\\ \end{matrix} \right|$ to get the required answer.

Complete step-by-step answer:
According to the problem, we are given that we need to find the area bounded by the lines $x+2y=2$, $y-x=1$ and $2x+y=7$.
Let us find the intersection point of the lines $x+2y=2$, $y-x=1$. Let us substitute $y=x+1$ in $x+2y=2$.
So, we have $x+2\left( x+1 \right)=2$.
$\Rightarrow x+2x+2=2$.
$\Rightarrow 3x=0$.
$\Rightarrow x=0$, let us substitute this value in $x+2y=2$.
So, we get $0+2y=2$.
$\Rightarrow 2y=2$.
$\Rightarrow y=1$.
So, the intersection point of the lines $x+2y=2$, $y-x=1$ is $A\left( 0,1 \right)$ ---(1).
Let us find the intersection point of the lines $x+2y=2$, $2x+y=7$. Let us substitute $y=7-2x$ in $x+2y=2$.
So, we have $x+2\left( 7-2x \right)=2$.
$\Rightarrow x+14-4x=2$.
$\Rightarrow -3x=-12$.
$\Rightarrow x=4$, let us substitute this value in $x+2y=2$.
So, we get $4+2y=2$.
$\Rightarrow 2y=-2$.
$\Rightarrow y=-1$.
So, the intersection point of the lines $x+2y=2$, $2x+y=7$ is $B\left( 4,-1 \right)$ ---(2).
Let us find the intersection point of the lines $2x+y=7$, $y-x=1$. Let us substitute $y=x+1$ in $2x+y=7$.
So, we have $2x+x+1=7$.
$\Rightarrow 3x=6$.
$\Rightarrow x=2$, let us substitute this value in $2x+y=7$.
So, we get $2\left( 2 \right)+y=7$.
$\Rightarrow 4+y=7$.
$\Rightarrow y=3$.
So, the intersection point of the lines $2x+y=7$, $y-x=1$ is $C\left( 2,3 \right)$ ---(3).
Let us draw the figure representing this information.

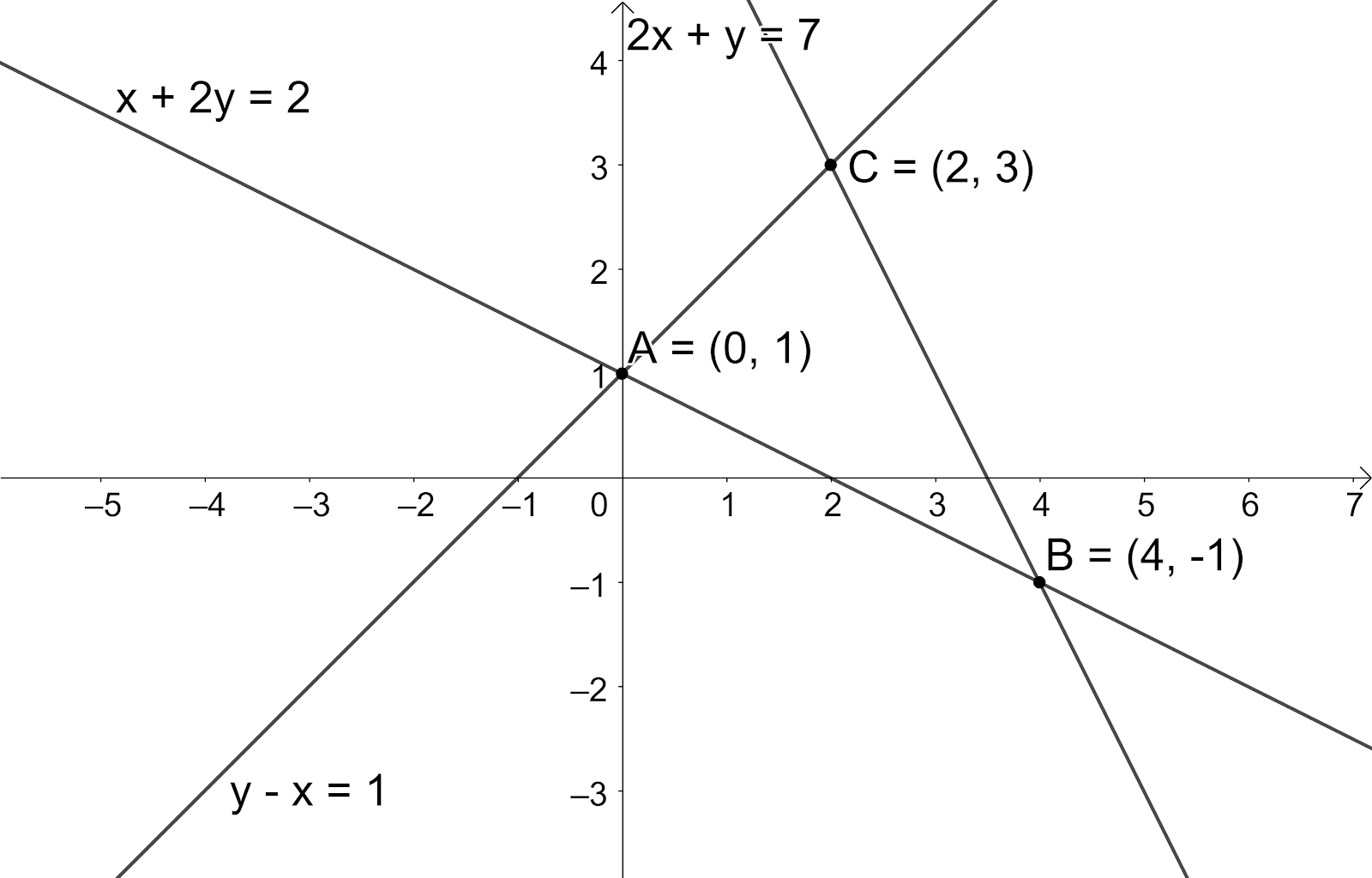
We know that the area of the triangle $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ is $A=\dfrac{1}{2}\left| \begin{matrix} {{x}_{1}}-{{x}_{2}} & {{x}_{1}}-{{x}_{3}} \\\ {{y}_{1}}-{{y}_{2}} & {{y}_{1}}-{{y}_{3}} \\\ \end{matrix} \right|$.
So, we get $A=\dfrac{1}{2}\left| \begin{matrix} 0-4 & 0-2 \\\ 1+1 & 1-3 \\\ \end{matrix} \right|$.
$\Rightarrow A=\dfrac{1}{2}\left| \begin{matrix} -4 & -2 \\\ 2 & -2 \\\ \end{matrix} \right|$.
We know that $\left| \begin{matrix} a & b \\\ c & d \\\ \end{matrix} \right|=\left( a\times d \right)-\left( b\times c \right)$.
$\Rightarrow A=\dfrac{1}{2}\left( \left( -4\times -2 \right)-\left( 2\times -2 \right) \right)$.
$\Rightarrow A=\dfrac{1}{2}\left( 8-\left( -4 \right) \right)$.
$\Rightarrow A=\dfrac{1}{2}\left( 8+4 \right)$.
$\Rightarrow A=\dfrac{1}{2}\left( 12 \right)$.
$\Rightarrow A=6$ sq.units.
∴ The area bounded by the lines $x+2y=2$, $y-x=1$ and $2x+y=7$ is 6 sq.units.

Note: We can also find the area of the triangle by finding the lengths of its sides and using the Heron’s formula $\left( \sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)} \right)$. We need to perform each step carefully in order to avoid confusion and calculation mistakes. We can also solve this problem by using the concept of area through integration between the intersection points. Similarly, we can expect problems to find the centre of the circumcircle of the obtained triangle.