Question

Find the area bounded by the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ and the ordinates x=0 and x=ae where ${{\text{b}}^2} = {{\text{a}}^2}\left( {1 - {e^2}} \right)$ and $e < 1$

Answer 1

First try to construct a diagram which is bounded by the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ and the ordinates x=0 and x=ae. Shade the region which is bounded by all these lines and curves. next try to find the intersection of the line and curves given. After this step construct a strip and integrate over the strip to get the entire area.

Complete step by step solution:
Let us first try to construct the ellipse given to us and the lines.
We know that line x=0 is nothing but the y-axis also line x=ae is a straight line passing through the point x=ae and parallel to y-axis.
To construct the diagram we will have to first calculate the intersection of given ellipse and the line x=ae
Since we have been given that $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$
$\Rightarrow \dfrac{{{y^2}}}{{{b^2}}} = 1 - \dfrac{{{x^2}}}{{{a^2}}} \\\ \Rightarrow \dfrac{{{y^2}}}{{{b^2}}} = \dfrac{{{a^2} - {x^2}}}{{{a^2}}} \\\ \Rightarrow {y^2} = \dfrac{{{a^2}}}{{{b^2}}}({a^2} - {x^2}) \\\$
Taking square root on both sides we get
$y = \sqrt {\dfrac{{{a^2}}}{{{b^2}}}({a^2} - {x^2})} \\\ \Rightarrow y = \pm \dfrac{a}{b}\sqrt {({a^2} - {x^2})} \\\$
$y = \sqrt {\dfrac{{{a^2}}}{{{b^2}}}({a^2} - {x^2})} \\\ \Rightarrow y = \pm \dfrac{a}{b}\sqrt {({a^2} - {x^2})} \\\$

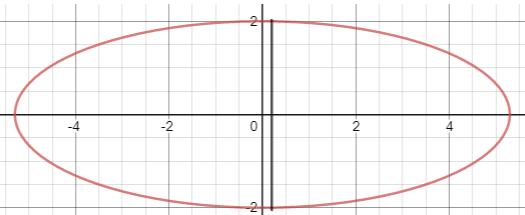
The above shaded region is the area to be found out. Since the area is the same above the x-axis and below the x-axis we will try to find the area above the x-axis and multiply it by 2 to get our entire area.
Since we are calculating the area in the first quadrant, y will be positive, hence $y = \dfrac{a}{b}\sqrt {{a^2} - {x^2}}$.
To calculate the area of the shaded region let us construct a vertical strip as shown in the figure constructed whose length is dx and distance is y.
Since this is a vertical strip we will have to integrate it over x
Therefore integrating we get
${\text{I = 2}}\int\limits_0^{ae} {\dfrac{b}{a}\sqrt {{a^2} - {b^2}} } dx \\\ = \dfrac{{2b}}{a}\int\limits_0^{ae} {\sqrt {{a^2} - {b^2}} } dx \\\$
Solving the integral we get
${\text{I = }}\dfrac{{2b}}{a}\left( {\dfrac{1}{2}x \times \sqrt {{a^2} - {x^2}} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}\dfrac{x}{a}} \right)_0^{ae} \\\ \Rightarrow {\text{I = }}\dfrac{{2b}}{a}\left[ {\dfrac{{ae}}{2}\sqrt {{a^2} - {a^2}{e^2}} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}\dfrac{{ae}}{a} - 0 + 0} \right] \\\$
Because $\left( {\dfrac{1}{2}0 \times \sqrt {{a^2} - 0} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}\dfrac{0}{a}} \right) = 0$
Solving further we get
${\text{I = }}\dfrac{{2b}}{a}\left[ {\dfrac{{ae\sqrt {{a^2}\left( {1 - {e^2}} \right)} }}{2} + \dfrac{{{a^2}{{\sin }^{ - 1}}e}}{2}} \right]$
since ${{\text{b}}^2} = {{\text{a}}^2}\left( {1 - {e^2}} \right)$, we get
${\text{I = }}\dfrac{{2b}}{a}\left[ {\dfrac{{aeb}}{2} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}e} \right] \\\ \Rightarrow {\text{I = }}{{\text{b}}^2}e + ab{\sin ^{ - 1}}e \\\ \Rightarrow {\text{I = ab}}\left[ {\dfrac{{{b^2}e}}{a} + {{\sin }^{ - 1}}e} \right] - - - (1) \\\$
Now since
${b^2} = {a^2}\left( {1 - {e^2}} \right) \\\ \Rightarrow \dfrac{{{b^2}}}{{{a^2}}} = \left( {1 - {e^2}} \right) \\\ \Rightarrow \dfrac{b}{a} = \sqrt {1 - {e^2}} \\\$
Substituting this in equation (1) we get
${\text{I = ab}}\left[ {e\sqrt {1 - {e^2}} + {{\sin }^{ - 1}}e} \right]$ this the final area of the shaded region.

Note:
When given this type of question try to first construct the diagram and shade the area enclosed by all the lines and curves given. This will initially help us to find a start to our solution. Try to select a vertical or a horizontal or a radial strip according to the requirement and the situation of the shaded area.