Question

Find the area bounded by the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ and the ordinates $x = 0$and $x = ae$, where ${b^2} = {a^2}\left( {1 - {e^2}} \right)$ and $e < 1$.

Answer 1

Hint: Simplify the given ellipse equation and integrate within the given ordinate limits to find the area.

An ellipse of the form $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ will meet the X-axis at (a, 0) and the Y-axis at (0, b). Let these points be P (a,0) and Q (0, b). It is symmetrical about the axes.
The ordinates given are $x = 0$and $x = ae$ which will be parallel to the Y-axis as shown in the figure.
The shaded area is the area bounded by the ellipse and the given ordinates.

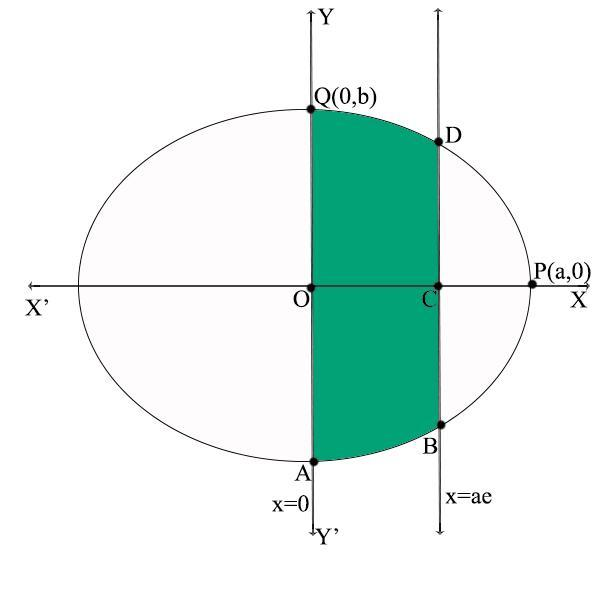
Required area = Area of the shaded region
= $2 \times$Area of QOCD
=$2 \times \int_0^{ae} y dx$ …(1)
The given equation is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$. Let us find the value of y from this equation and substitute in equation (1).
\begin{gathered} \dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1 \\\ \begin{array}{*{20}{l}} \begin{gathered} \dfrac{{{y^2}}}{{{b^2}}} = 1 - \dfrac{{{x^2}}}{{{a^2}}} \\\ \dfrac{{{y^2}}}{{{b^2}}} = \dfrac{{{a^2} - {x^2}}}{{{a^2}}} \\\ \end{gathered} \\\ {{y^2} = \dfrac{{{b^2}}}{{{a^2}}}\left( {{a^2} - {x^2}} \right)} \\\ {y = \pm \sqrt {\dfrac{{{b^2}}}{{{a^2}}}\left( {{a^2} - {x^2}} \right)} } \\\ {y = \pm \dfrac{b}{a}\sqrt {\left( {{a^2} - {x^2}} \right)} } \end{array} \\\ \end{gathered}
Since, the area in equation (1) which is the area of QOCD is in the 1st quadrant. Hence, the value of y will be positive.
Hence, $y = \dfrac{b}{a}\sqrt {\left( {{a^2} - {x^2}} \right)}$ …(2)
Substituting (2) in (1),
Required area =$2 \times \int_0^{ae} y dx$

{ = 2\mathop \smallint \limits_0^{ae} \dfrac{b}{a}\sqrt {{a^2} - {x^2}} dx} \\\ { = \dfrac{{2b}}{a}\mathop \smallint \limits_0^{ae} \sqrt {{a^2} - {x^2}} dx} \end{array}$$ (Since a and b are constants) We know that, $$\mathop \smallint \nolimits^ \sqrt {{a^2} - {x^2}} dx = \dfrac{{x\sqrt {{a^2} - {x^2}} }}{2} + \dfrac{{{a^2}}}{2}{\sin ^{ - 1}}(\dfrac{x}{a}) + c$$ Using this in the previous step, we get Required area = $$\dfrac{{2b}}{a}[\dfrac{1}{2}x\sqrt {{a^2} - {x^2}} + \dfrac{{{a^2}}}{2}{\sin ^{ - 1}}\dfrac{x}{a}]_0^{ae}$$ $$\begin{gathered} \begin{array}{*{20}{l}} { = \dfrac{{2b}}{a}[(\dfrac{{ae}}{2}\sqrt {{a^2} - {{(ae)}^2}} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}\dfrac{{ae}}{a}) - (\dfrac{0}{2}\sqrt {{a^2} - 0} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}(\dfrac{0}{a}))]} \\\ { = \dfrac{{2b}}{a}[\dfrac{{ae}}{2}\sqrt {{a^2} - {a^2}{e^2}} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}(e) - 0 - \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}(0)]} \\\ { = \dfrac{{2b}}{a}[\dfrac{{ae}}{2} \cdot a\sqrt {1 - {e^2}} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}e - 0]} \end{array} \\\ \begin{array}{*{20}{l}} { = \dfrac{{2b}}{a}[\dfrac{{{a^2}e}}{2}\sqrt {1 - {e^2}} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}e]} \\\ { = \dfrac{{2b}}{a}(\dfrac{{{a^2}}}{2})[e\sqrt {1 - {e^2}} + {{\sin }^{ - 1}}e]} \\\ { = ab[e\sqrt {1 - {e^2}} + {{\sin }^{ - 1}}e]} \end{array} \\\ \end{gathered} $$ Required Area bounded by the ellipse $$\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$$ and the ordinates $x = 0$and $x = ae$ $$ = ab[e\sqrt {1 - {e^2}} + {\sin ^{ - 1}}e]$$ Note: The required area can also be found by integrating the entire shaded area QOABCD instead of finding $2 \times $Area of QOCD. It would be a little lengthier and more unnecessary because the given ellipse is symmetrical about the origin.