Question

Find the area bounded by the curve $y = 4x\left( {x - 1} \right)\left( {x - 2} \right)$

Answer 1

Hint : The points where the value of the function is $0$ is to be determined by putting $y = 0$ and calculating the $x$ values of the curve are to be determined and the function should be evaluated between the lower and upper limit for the function.

Complete step-by-step answer :
The given function is
$y = 4x\left( {x - 1} \right)\left( {x - 2} \right)$
Put $y = 0$
$4x\left( {x - 1} \right)\left( {x - 2} \right)$ =0
The critical values are $x = 0,1,2$ . These are the values at which the function attains 0 value.

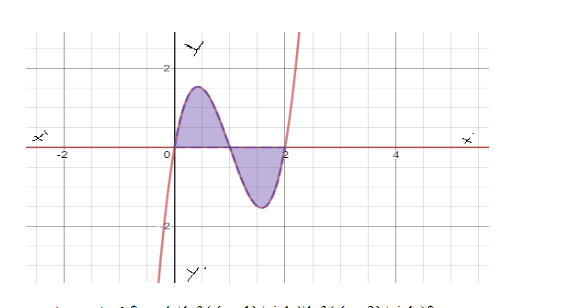
Fig. The graph of $y = 4x\left( {x - 1} \right)\left( {x - 2} \right)$
The graph of the given function above, confirms the values as $x = 0,1,2$ where the function attains 0 value.
To find the area under the curve , integrate the function $y = 4{x^3} - 12{x^2} + 8x$ between the limits $x = 0$ and $x = 2$ .
$\Rightarrow I = \int\limits_0^2 {\left( {4{x^3} - 12{x^2} + 8x} \right)} dx$
On integrating the function,

$$\Rightarrow I = \left[ {\dfrac{{4{x^4}}}{4} - \dfrac{{12{x^3}}}{3} + \dfrac{{8{x^2}}}{2}} \right]_0^2 \\\ \Rightarrow I = \left[ {{x^4} - 4{x^3} + 4{x^2}} \right]_0^2 \\\ \Rightarrow I = \left[ {\left( {{2^4} - 4{{\left( 2 \right)}^3} + 4{{\left( 2 \right)}^2}} \right) - \left( {0 - 0 + 0} \right)} \right] \\\ \Rightarrow I = \left[ {16 - 32 + 16} \right] \\\ \Rightarrow I = 0 \\\$$

Hence, the area under the curve is $0$ .
It implies that the area above the $x$ - axis is the same as the area below the $x$ - axis.

Note : The important points which needs to be remembered are as follows,
The integration of the function between the prescribed limits gives the area under the curve.
For instance, the area under the curve for $\sin x$ from $0 - \dfrac{\pi }{2}$ is $1$ square units and from $0 - \pi$ is $2$ square units and from $0 - 2\pi$ is $0.$
The values where the function attains $0$ values should be carefully evaluated .These points are evaluated either by drawing the graph of the function if possible or putting the value of $y = 0$ . By doing this observe the value $x$ where functions attains $0$ values.