Question

Find the area bounded by the curve ${{x}^{2}}=4y$ and the line $x=4y-2$.

Answer 1

First of all, we should draw the graph which represents the curve ${{x}^{2}}=4y$ and the line $x=4y-2$. Now we should find the intersection points of the curve ${{x}^{2}}=4y$ and the line $x=4y-2$. To find the intersection point of curve ${{x}^{2}}=4y$ and the line $x=4y-2$, we have to substitute $x=4y-2$ in ${{x}^{2}}=4y$. After finding the intersection points, we have to integrate the given curve and line from the obtained limits. This gives us the area of the curve ${{x}^{2}}=4y$ and the line $x=4y-2$.

Complete step-by-step answer :
First of all, we should draw the graph which represents the curve ${{x}^{2}}=4y$ and the line $x=4y-2$.

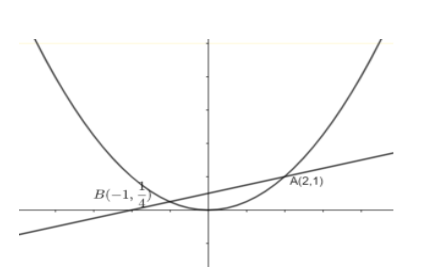
Now we should find the intersection points of the curve ${{x}^{2}}=4y$ and the line $x=4y-2$.
To find the intersection point of curve ${{x}^{2}}=4y$ and the line $x=4y-2$, we have to substitute $x=4y-2$ in ${{x}^{2}}=4y$.

& \Rightarrow {{\left( 4y-2 \right)}^{2}}=4y \\\ & \Rightarrow 16{{y}^{2}}-16y+4=4y \\\ & \Rightarrow 16{{y}^{2}}-20y+4=0 \\\ & \Rightarrow 4(4{{y}^{2}}-5y+1)=0 \\\ \end{aligned}$$ Now let us divide both sides by 4, then we get $$\begin{aligned} & \Rightarrow 4{{y}^{2}}-5y+1=0 \\\ & \Rightarrow 4{{y}^{2}}-4y-y+1=0 \\\ & \Rightarrow 4y\left( y-1 \right)-1\left( y-1 \right)=0 \\\ & \Rightarrow \left( 4y-1 \right)\left( y-1 \right)=0 \\\ \end{aligned}$$ Case 1: $$\begin{aligned} & \Rightarrow 4y-1=0 \\\ & \Rightarrow 4y=1 \\\ & \Rightarrow y=\dfrac{1}{4}.....(1) \\\ \end{aligned}$$ Now let us substitute $$y=\dfrac{1}{4}$$in $${{x}^{2}}=4y$$. $$\begin{aligned} & \Rightarrow {{x}^{2}}=4\left( \dfrac{1}{4} \right) \\\ & \Rightarrow {{x}^{2}}=1 \\\ & \Rightarrow x=\pm 1....(2) \\\ \end{aligned}$$ So, from equation (1) and equation (2), it is clear that $$\left( -1,\dfrac{1}{4} \right),\left( 1,\dfrac{1}{4} \right)$$ are intersection points of the curve $${{x}^{2}}=4y$$ and the line $$x=4y-2$$. Now let us substitute $$\left( -1,\dfrac{1}{4} \right)$$ in $$x=4y-2$$. $$\begin{aligned} & \Rightarrow -1=4\left( \dfrac{1}{4} \right)-2 \\\ & \Rightarrow -1=-1 \\\ \end{aligned}$$ So, it is clear that $$\left( -1,\dfrac{1}{4} \right)$$ is the intersection point of the curve $${{x}^{2}}=4y$$ and the line $$x=4y-2$$. Now let us substitute $$\left( 1,\dfrac{1}{4} \right)$$ in $$x=4y-2$$. $$\begin{aligned} & \Rightarrow 1=4\left( \dfrac{1}{4} \right)-2 \\\ & \Rightarrow 1=-1 \\\ \end{aligned}$$ We know that this is not possible. So, we can say that $$\left( 1,\dfrac{1}{4} \right)$$ is not the intersection point of the curve $${{x}^{2}}=4y$$ and the line $$x=4y-2$$. Case 2: $$\begin{aligned} & \Rightarrow y-1=0 \\\ & \Rightarrow y=1.....(3) \\\ \end{aligned}$$ Now let us substitute $$y=1$$in $${{x}^{2}}=4y$$. $$\begin{aligned} & \Rightarrow {{x}^{2}}=4 \\\ & \Rightarrow x=\pm 2....(4) \\\ \end{aligned}$$ So, from equation (3) and equation (4), it is clear that $$\left( 2,1 \right),\left( -2,1 \right)$$ are intersection points of the curve $${{x}^{2}}=4y$$ and the line $$x=4y-2$$. Now let us substitute $$\left( -2,1 \right)$$ in $$x=4y-2$$. $$\begin{aligned} & \Rightarrow -2=4\left( 1 \right)-2 \\\ & \Rightarrow -2\ne 2 \\\ \end{aligned}$$ So, it is clear that $$\left( -2,1 \right)$$ is not the intersection point of the curve $${{x}^{2}}=4y$$ and the line $$x=4y-2$$ Now let us substitute $$\left( 2,1 \right)$$ in $$x=4y-2$$. $$\begin{aligned} & \Rightarrow 2=4\left( 1 \right)-2 \\\ & \Rightarrow 2=2 \\\ \end{aligned}$$ So, it is clear that $$\left( 2,1 \right)$$ is the intersection point of the curve $${{x}^{2}}=4y$$ and the line $$x=4y-2$$. From above we can say that $$\left( 2,1 \right)$$ and $$\left( -1,\dfrac{1}{4} \right)$$ are the intersection points of the curve $${{x}^{2}}=4y$$ and the line $$x=4y-2$$. Now we have to calculate the area bounded by the curve $${{x}^{2}}=4y$$ and the line $$x=4y-2$$. from $$\left( 2,1 \right)$$ to $$\left( -1,\dfrac{1}{4} \right)$$. Let us assume this area is equal to I. $$\begin{aligned} & \Rightarrow I=\int\limits_{-1}^{2}{\left( \dfrac{x+2}{4} \right)-\left( \dfrac{{{x}^{2}}}{4} \right)} \\\ & \Rightarrow I=\int\limits_{-1}^{2}{\dfrac{x+2-{{x}^{2}}}{4}} \\\ & \Rightarrow I=\left( \dfrac{1}{4} \right)\int\limits_{-1}^{2}{\left( x+2-{{x}^{2}} \right)} \\\ \end{aligned}$$ We know that $$\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}$$ $$\begin{aligned} & \Rightarrow I=\left( \dfrac{1}{4} \right)\left[ \dfrac{{{x}^{2}}}{2}+2x-\dfrac{{{x}^{3}}}{3} \right]_{-1}^{2} \\\ & \Rightarrow I=\left( \dfrac{1}{4} \right)\left[ \left( \dfrac{{{2}^{2}}}{2}+2(2)-\dfrac{{{2}^{3}}}{3} \right) \right]-\left( \dfrac{1}{2}-2(1)+\dfrac{1}{3} \right) \\\ & \Rightarrow I=\left( \dfrac{1}{4} \right)\left[ \left( 2+4-\dfrac{8}{3} \right)-\left( \dfrac{1}{2}-2+\dfrac{1}{3} \right) \right] \\\ & \Rightarrow I=\left( \dfrac{1}{4} \right)\left[ 8-\dfrac{8}{3}-\dfrac{5}{6} \right] \\\ & \Rightarrow I=\left( \dfrac{1}{4} \right)\left[ 8-\dfrac{21}{6} \right] \\\ & \Rightarrow I=\left( \dfrac{1}{4} \right)\left( \dfrac{27}{6} \right) \\\ & \Rightarrow I=\dfrac{9}{8} \\\ \end{aligned}$$ So, it is clear that the area bounded by the curve $${{x}^{2}}=4y$$ and the line $$x=4y-2$$ is $$\dfrac{9}{8}$$. **Note** : Students may assume that $$\left( -2,1 \right)$$ and $$\left( 1,\dfrac{1}{4} \right)$$ are the intersection points of the curve $${{x}^{2}}=4y$$ and the line $$x=4y-2$$. If this is done, then we can get the correct area. We can identify whether the intersection points are correct by having a look at the graph. The graph will give us a clear view in which points we have to calculate the area. Students should be careful while applying integration formulas in the solution. Students should also be careful in the calculation part of the problem.