Question

Find the area bounded by the circle the circle ${{x}^{2}}+{{y}^{2}}=16$ and the line y = x in the first quadrant.

Answer 1

Hint: First draw the graph of the circle ${{x}^{2}}+{{y}^{2}}=16$ and assume that it is intersecting the line y = x at point x = a in the first quadrant. To determine this point of intersection, solve the two equations. Now, to find the area of the region, we have to consider two parts of integration. The first part is the integration of function y = x from the limits 0 to ‘a’. The second part contains the integration of the function $y=\sqrt{16-{{x}^{2}}}$ from the limits ‘a’ to the point (say b) where the circle meets the positive x-axis. Therefore, $A=\int_{0}^{a}{xdx+\int_{a}^{b}{\sqrt{16-{{x}^{2}}}}dx}$, where A is the area of the required region, ‘a’ is the x-coordinate of point of intersection of the circle and line in the first quadrant and ‘b’ is the x-coordinate of the point where the circle meets the positive x-axis.

Complete step-by-step answer:
Let us draw the graph of line y = x and the circle ${{x}^{2}}+{{y}^{2}}=16$.

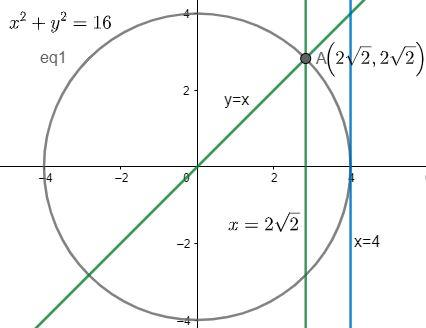
Now, let us determine the point of intersection of the given circle and the line. We have two equations,
$y=x......................(i)$
${{x}^{2}}+{{y}^{2}}=16..................(ii)$
Therefore, substituting the value of y from equation (i) in equation (ii), we get,
$\begin{aligned} & {{x}^{2}}+{{x}^{2}}=16 \\\ & \Rightarrow 2{{x}^{2}}=16 \\\ & \Rightarrow {{x}^{2}}=8 \\\ \end{aligned}$
Taking the square root both sides, we get,
$x=\pm 2\sqrt{2}$
Since, we are considering the point in first quadrant, therefore, the value of x must be positive. Hence,
$x=2\sqrt{2}$. So, the value of ‘a’ is $2\sqrt{2}$.
Let us determine the point where the circle meets x-axis.
The point at which the circle will meet x-axis will have its y-coordinate equal to 0. Therefore, substituting y = 0 in equation ${{x}^{2}}+{{y}^{2}}=16$, we get,
${{x}^{2}}=16$
Taking square root both sides, we get,
$\begin{aligned} & x=\pm \sqrt{16} \\\ & \Rightarrow x=\pm 4 \\\ \end{aligned}$
Since this point is in the first quadrant, therefore, x must be positive. Hence,
$x=4$. So, the value of ‘b’ is 4.
Therefore, total area of the region is,
$\begin{aligned} & A=\int_{0}^{a}{xdx+\int_{a}^{b}{\sqrt{16-{{x}^{2}}}}dx} \\\ & A=\int_{0}^{2\sqrt{2}}{xdx+\int_{2\sqrt{2}}^{4}{\sqrt{16-{{x}^{2}}}}dx} \\\ \end{aligned}$
This can be written as:
$A=\int_{0}^{2\sqrt{2}}{xdx+\int_{2\sqrt{2}}^{4}{\sqrt{{{\left( 4 \right)}^{2}}-{{x}^{2}}}}dx}$
We have to evaluate the first integral using the formula: $\int{{{x}^{a}}dx}=\dfrac{{{x}^{a+1}}}{a+1}$. The second integral is of the is of the form $\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx}$, whose value is $\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a}$. Using these formulas, we get,
$A=\left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{2\sqrt{2}}+\left[ \dfrac{x}{2}\sqrt{{{\left( 4 \right)}^{2}}-{{x}^{2}}}+\dfrac{{{\left( 4 \right)}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{4} \right]_{2\sqrt{2}}^{4}$
Substituting the value of limits, we get,

& A=\left[ \dfrac{{{\left( 2\sqrt{2} \right)}^{2}}}{2}-\dfrac{{{0}^{2}}}{2} \right]+\left[ \left( \dfrac{4}{2}\sqrt{{{\left( 4 \right)}^{2}}-{{\left( 4 \right)}^{2}}}+\dfrac{{{\left( 4 \right)}^{2}}}{2}{{\sin }^{-1}}\dfrac{4}{4} \right)-\left( \dfrac{2\sqrt{2}}{2}\sqrt{{{\left( 4 \right)}^{2}}-{{\left( 2\sqrt{2} \right)}^{2}}}+\dfrac{{{\left( 4 \right)}^{2}}}{2}{{\sin }^{-1}}\dfrac{2\sqrt{2}}{4} \right) \right] \\\ & \Rightarrow A=4+\left( \dfrac{4}{2}\times 0+\dfrac{16}{2}{{\sin }^{-1}}1 \right)-\left( \sqrt{2}\times \sqrt{8}+\dfrac{16}{2}{{\sin }^{-1}}\dfrac{1}{\sqrt{2}} \right) \\\ & \Rightarrow A=4+8{{\sin }^{-1}}1-4-8{{\sin }^{-1}}\dfrac{1}{\sqrt{2}} \\\ \end{aligned}$$ We know that ${{\sin }^{-1}}1=\dfrac{\pi }{2}$ and ${{\sin }^{-1}}\dfrac{1}{\sqrt{2}}=\dfrac{\pi }{4}$. Therefore, substituting these values we get, $\begin{aligned} & A=4+8\times \dfrac{\pi }{2}-4-8\times \dfrac{\pi }{4} \\\ & \Rightarrow A=4\pi -2\pi \\\ & \Rightarrow A=2\pi \ \text{sq}\text{.units} \\\ \end{aligned}$ Note: One may note that we can check our answer by finding the area directly with the formula $A=\dfrac{\pi {{r}^{2}}}{8}$, where ‘r’ is the radius of the circle. We have divided the area of the circle by 8 because the area which we have to determine is half of the area of a quadrant, that means half of $\dfrac{\pi {{r}^{2}}}{4}$. Remember that do not solve the question by this direct method because we have been asked to use integration in the question. This direct method is only to check the answer.