Question

Find the area and the perimeter of quadrilateral ABCD, if AB = 8 cm, AD = 10 cm, BD = 12 cm, DC = 13 cm and $\angle DBC=90{}^\circ$.

A. $69.7c{{m}^{2}}$ and $36cm$
B. $69.7c{{m}^{2}}$ and $38.97cm$
C. $88.63c{{m}^{2}}$ and $36cm$
D. None of these

Answer 1

Hint: We will assume quadrilateral ABCD as the sum of two triangles ABD and DBC. We will then find the area of triangle ABD by using the formula $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$, where $s=\dfrac{a+b+c}{2}$ and a, b, c are the sides of the triangle. We will also use the formula for the area of a triangle, $\dfrac{1}{2}\times base\times height$ to find the area of triangle DBC. We will get the area of the quadrilateral by adding the areas of the two triangles. We will finally find the perimeter of the given quadrilateral by finding the sum of all its sides, (AB + BC + CD + DA).

Complete step-by-step answer:

It is given in the question that we have to find the area and perimeter of quadrilateral ABCD, if AB = 8 cm, AD = 10 cm, BD = 12 cm, DC = 13 cm and $\angle DBC=90{}^\circ$.

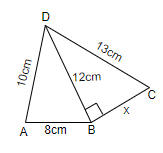
We will first try to find the area of triangle ABD by using the formula $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$, where $s=\dfrac{a+b+c}{2}$ and a, b, c are the sides of the triangle. IN this triangle, we have the sides as, a = 8 cm, b = 10 cm and c = 12 cm. So, we can put these values in the formula to get s. So, we get,
$\begin{aligned} & s=\dfrac{8+10+12}{2} \\\ & \Rightarrow s=\dfrac{30}{2} \\\ & \Rightarrow s=15 \\\ \end{aligned}$
Now, we will apply this value in the formula for area. So, we get the area of triangle ABD as,
$\begin{aligned} & =\sqrt{15\left( 15-8 \right)\left( 15-10 \right)\left( 15-12 \right)} \\\ & \Rightarrow \sqrt{15\left( 7 \right)\left( 5 \right)\left( 3 \right)} \\\ & \Rightarrow \sqrt{15\times 15\times 7} \\\ & \Rightarrow \sqrt{1575} \\\ & \Rightarrow 39.68c{{m}^{2}} \\\ \end{aligned}$
Now, we know that triangle BDC is a right angled triangle, right angled at $\angle B$. We know that the Pythagoras theorem states that in a right angled triangle, the sum of the square of the base and height is equal to the square of its hypotenuse. So, by using Pythagoras theorem, we can say that, in triangle DBC, we have,
${{\left( DB \right)}^{2}}+{{\left( BC \right)}^{2}}={{\left( DC \right)}^{2}}$
We know that DB = 12 cm, DC = 13 cm. SO, we will assume BC = x. SO, we will then get,
$\begin{aligned} & {{\left( 12 \right)}^{2}}+{{\left( x \right)}^{2}}={{\left( 13 \right)}^{2}} \\\ & \Rightarrow {{\left( x \right)}^{2}}={{\left( 13 \right)}^{2}}-{{\left( 12 \right)}^{2}} \\\ & \Rightarrow {{\left( x \right)}^{2}}=169-144 \\\ & \Rightarrow {{x}^{2}}=25 \\\ & \Rightarrow x=\sqrt{25} \\\ & \Rightarrow x=5 \\\ \end{aligned}$
So, we get the length of BC as 5 cm. Now, we know that the area of a triangle is $\dfrac{1}{2}\times base\times height$. So, in triangle BDC, we have the base = 5 cm, and the height = 12 cm. So, we get the area as,
$\begin{aligned} & =\dfrac{1}{2}\times 5\times 12 \\\ & \Rightarrow 5\times 6 \\\ & \Rightarrow 30c{{m}^{2}} \\\ \end{aligned}$
Now, we know that the area of the quadrilateral will be equal to the area of triangle ABD + area of triangle BDC. So, putting the vales, we get,
$\begin{aligned} & =\left( 39.68+30 \right)c{{m}^{2}} \\\ & \Rightarrow 69.68c{{m}^{2}} \\\ & \Rightarrow 69.7c{{m}^{2}} \\\ \end{aligned}$
We know that the perimeter of the quadrilateral = the sum of all the sides of the quadrilateral ABCD = (AB + BC + CD + DA). We have all the values for the sides, so we get the perimeter as,
= (8 + 5 + 13 + 10) cm = 36 cm.
So, we have got the area of the quadrilateral as $69.7c{{m}^{2}}$ and the perimeter as 36 cm.
Hence, option A is the correct answer.

Note: Most of the students assume $\angle DAB=90{}^\circ$ as it appears as one in the figure, but one should not assume like that unless specified in the question. That would lead to an incorrect answer. The students should also remember the formula of area of triangle, when sides are given is, $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ where $s=\dfrac{a+b+c}{2}$ and a, b, c are the sides of the triangle and also when the other dimensions are like base and height are given, then they should use the formula, $\dfrac{1}{2}\times base\times height$.