Question

Find the apparent weight of a man weight 49 kg on earth where he is standing in a life which is irising with an acceleration of $1.2{m}/{{{s}^{2}}}\;$ii) going with the same acceleration iii) falling freely the action gravity iv) going up down with uniform velocity. Given $9.8{m}/{{{s}^{2}}}\;$

Answer 1

The question is based on the concept of the force acting on the body. So we will make use of the free body diagram to solve this type of question. We will solve all the four sub-parts using the formulae of the forces acting on the body, such as the normal force and the frictional force.

Formula used:
$N=ma$

Complete step by step solution:
The free-body diagram of the man standing in a lift is given as follows.

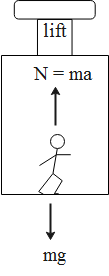
The normal force acting on the body is given as follows.
$N=ma$
Where m is the mass of the body and a is the acceleration of the body.
(i) rising with an acceleration of $1.2{m}/{{{s}^{2}}}\;$.
The formula for computing the apparent weight when the lift is rising with an acceleration of$1.2{m}/{{{s}^{2}}}\;$ is as follows.
$F=mg+ma$
Where m is the mass of the man, a is the acceleration of the lift and g is the gravitational constant.
Substitute the values in the above equation.

& F=m(a+g) \\\ & F=49(1.2+9.8) \\\ & F=539\,N \\\ \end{aligned}$$ Therefore, the apparent weight of the man standing in a lift will be, $$\begin{aligned} & M=\dfrac{539}{9.8} \\\ & M=55\,kgf \\\ \end{aligned}$$ (ii) going down with the same acceleration The formula for computing the apparent weight when the lift is going down with an acceleration of$$1.2{m}/{{{s}^{2}}}\;$$ is as follows. $$F=mg-ma$$ Where m is the mass of the man, a is the acceleration of the lift and g is the gravitational constant. Substitute the values in the above equation. $$\begin{aligned} & F=m(g-a) \\\ & F=49(9.8-1.2) \\\ & F=421.4\,N \\\ \end{aligned}$$ Therefore, the apparent weight of the man standing in a lift will be, $$\begin{aligned} & M=\dfrac{421.4}{9.8} \\\ & M=43\,kgf \\\ \end{aligned}$$ (iii) falling freely under gravity The formula for computing the apparent weight when the lift is falling freely under gravity $$\begin{aligned} & mg-N=mg \\\ & N=0 \\\ \end{aligned}$$ Where m is the mass of the man, a is the acceleration of the lift and g is the gravitational constant. Therefore, the apparent weight of the man standing in a lift will be, $$\begin{aligned} & M=\dfrac{0}{9.8} \\\ & M=0\,kgf \\\ \end{aligned}$$ (iv) going up or down with uniform velocity The formula for computing the apparent weight when the lift is going up or down with uniform velocity is as follows. $$F=mg-ma$$ Where m is the mass of the man, a is the acceleration of the lift and g is the gravitational constant. Substitute the values in the above equation. $$\begin{aligned} & F=m(g-a) \\\ & F=49(9.8-0) \\\ & F=480.2\,N \\\ \end{aligned}$$ Therefore, the apparent weight of the man standing in a lift will be, $$\begin{aligned} & M=\dfrac{480.2}{9.8} \\\ & M=49\,kgf \\\ \end{aligned}$$ $$\therefore $$ The apparent weight of a man standing in a lift when (i) rising with an acceleration of $$1.2{m}/{{{s}^{2}}}\;$$is 55 kgf, (ii) going down with the same acceleration is 43 kgf, (iii) falling freely under gravity is 0 and (iv) going up or down with uniform velocity is 49 kgf. **Note:** Using a free body diagram makes it easy to solve this type of question by understanding the forces acting on the body and the directions of the force. The units of the parameters should be taken care of.