Question

Find the angle which the line joining the points $\left( 1,\sqrt{3} \right)\ and\ \left( \sqrt{2},\sqrt{6} \right)$ makes with the x-axis.

Answer 1

Hint: First find out the slope of the line passing through two given points using the formula $\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)$ , Now use the fact that the slope of the line x-axis is nothing but zero.

Complete step-by-step answer:

Now, we have been given two points as $\left( 1,\sqrt{3} \right)\ and\ \left( \sqrt{2},\sqrt{6} \right)$. We have to find the angle which this line makes with the x–axis.

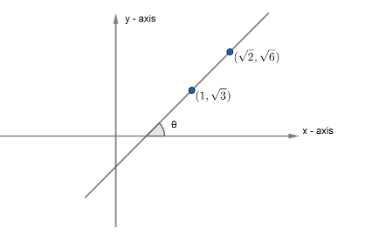
Now, we know that the slope of a line passing through two point $\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)$ is
$m=\tan \theta =\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
So, we have the slope of given line as,
$\tan \theta =\dfrac{\sqrt{6}-\sqrt{3}}{\sqrt{2}-1}$
Now, we take $\sqrt{3}$ common in numerator. So,
$\begin{aligned} & \tan \theta =\dfrac{\sqrt{3}\left( \sqrt{2}-\sqrt{1} \right)}{\sqrt{2}-1} \\\ & \tan \theta =\sqrt{3} \\\ \end{aligned}$
Now, we know that,
$\tan \left( \dfrac{\pi }{3} \right)=\sqrt{3}$
So, we have,
$\tan \theta =\tan \left( \dfrac{\pi }{3} \right)$
Therefore, the value of $\theta \ is\ \dfrac{\pi }{3}$.
Now, we know that the tangent of the angle which the line makes with the positive x – axis is slope. Hence, the angle which the given line makes with the x–axis is $\dfrac{\pi }{3}$.

Note: Angle between the lines with the given slopes can be found by using the formula $\theta ={{\tan }^{-1}}\left[ \left| \dfrac{x-y}{1-x\cdot y} \right| \right]$
(where $\theta$ is the angle between the two lines with slopes as x and y), Also keep in mind that any line parallel to the x-axis will always have its slope equal to zero.