Question

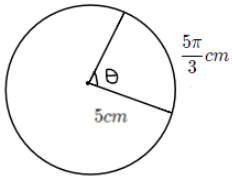
Find the angle subtended at the centre of the circle of radius 5cm by an arc of length $\dfrac{{5\pi }}{3}cm$.

Answer 1

Hint: Here we solve the problem by comparing the given length of arc with the length of arc formula from which we can obtain the angle subtended at the centre of the given circle.

Complete step by step answer:
Here the given length of arc is $\dfrac{{5\pi }}{3}cm$.
Given a circle of radius (r) = 5cm.
We know that the formula of length of arc =$\dfrac{\theta }{{{{360}^ \circ }}}\left( {2\pi r} \right)$ where $\theta$ is angle subtended at centre and $2\pi r$ is the circumference of circle.
So, here let us equate the given length of arc with its formula to get the angle subtended at the centre of the circle.
Therefore
$\Rightarrow \dfrac{{5\pi }}{3} = \dfrac{\theta }{{{{360}^ \circ }}} \times 2\pi r$
$\Rightarrow \dfrac{{5\pi }}{3} = \dfrac{\theta }{{{{360}^ \circ }}} \times 2\pi \times 5$ $\left( {\because r = 5} \right)$
On further simplification we get
$\Rightarrow \theta = \dfrac{{{{360}^ \circ }}}{6}$
$\Rightarrow \theta = {60^ \circ }$

Therefore the angle subtended at the centre of the circle is ${60^ \circ }$.

NOTE: In the above problem we have compared the given value of length of arc with the formula of length of arc to get the theta value which is the angle subtended at the centre of the circle. Generally we forget to substitute the value of r with the radius of the circle which is mandatory to get the theta value.