Question

Find the angle of intersection of the following curves.$\ y^{2} = x$ and $x^{2} = y$.

Answer 1

In this question, we need to find the angle of intersection of the two given curves. In order to find the angle of intersection, first we need to find the point of intersection of the two given curves. Then we need to find the slope of both the curves. By finding this, we can find the angle of intersection of the curves.

Complete step-by-step solution:
Given ,
$y^{2} = x$ ……………………………….(1)
$x^{2} = y$ ……………………………… (2)
By substituting (2) in (1),
We get,
$\left( x^{2} \right)^{2} = x$
$x^{4} = x$
By bringing all the terms to one side,
We get,
$x^{4} – x = 0$
Taking $x$ as common,
$x\left( x^{3} – 1 \right) = 0$
Thus we get the value of $x$ as
$\ (x = 0) \ or\ (x^{3} – 1 = 0)$
By simplifying,
We get,
$\ (x = 0)\ or\ (x^{3} = 1)$
Thus we get the values of $x$ are $0$ and $1$
Substituting the values of $x$ in (2)
We get,
$y = 0$ or $y = 1$
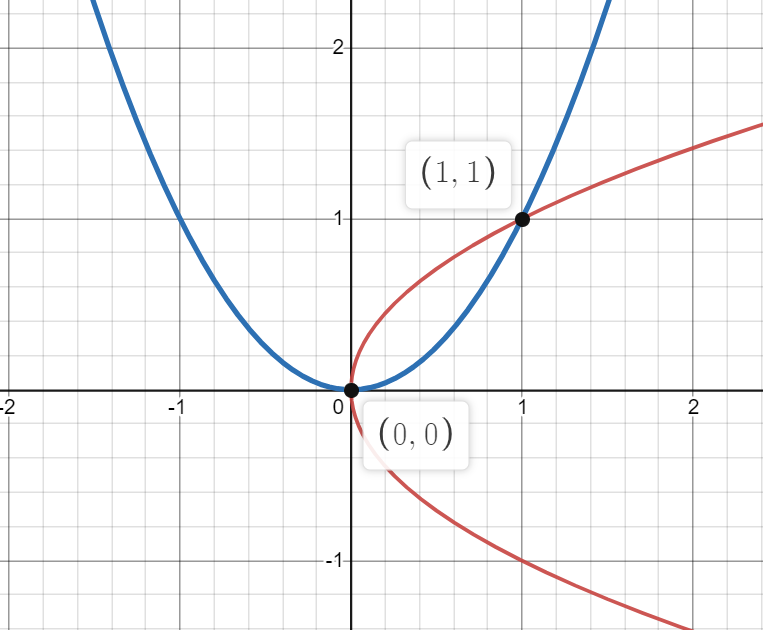
Therefore the point of intersection are $(0,\ 0)$ and$\ (1,\ 1)$
Then we have differentiate the given curves,
From (1),
$y^{2} = x$
Differentiating (1) w.r.t to x
$2y\left( \dfrac{{dy}}{{dx}} \right) = 1$
$\dfrac{{dy}}{{dx}} = \dfrac{1}{2y}$
Differentiating (2) w.r.t to x
$2x = \dfrac{{dy}}{{dx}}$
At $(0,\ 0)\$, the slope of the tangent to the curve $y^{2} = x$ is parallel to the $y – axis$ and the tangent to the curve $x^{2} = y$ is parallel to $x – axis$.
At $(1,\ 1)$, slope of the tangent to the curve $y^{2}\ = \ x$ is equal to $\dfrac{1}{2}$ and that of $x^{2}\ = \ y$ is $2$.
Thus we get,
$m{_1}= \dfrac{1}{2}$
$m{_2}= 2$
If $\theta$ is the angle of intersection of the curves,
$tan\theta = \ |\dfrac{(m{_1}m{_2})}{(1 + m{_1}m{_2})}|$
By substituting the values,
We get,
$tan\theta = \left| \dfrac{\left( 1\right)}{2} \right|$
$tan\theta = \left| \left( \dfrac{1}{2} \right)\right|$
Thus
$\theta = \tan^{- 1}\left( \dfrac{1}{2} \right)$
Final answer :
The angle of intersection is $\tan^{- 1}\left(\dfrac{1}{2} \right)$

Note: The concept used to find the angle of intersection is tangents and the normal. The angle of intersection is nothing but the angle of the line formed with the horizontal. The formula for the angle of intersection is $\tan \theta = m$