Question

Find the angle of elevation of the Sun when the shadow of a pole h m high is $\sqrt 3 h\;{\text{m}}$ long.

Answer 1

Hint : The upwards angle from the horizontal axis from the observer to the point of interest is known as the angle of elevation. With the help of the given conditions draw the perfect diagram and apply trigonometric functions accordingly. Here, we will use tangent function since we are given the measures of the opposite and the adjacent sides.

Complete step-by-step answer :

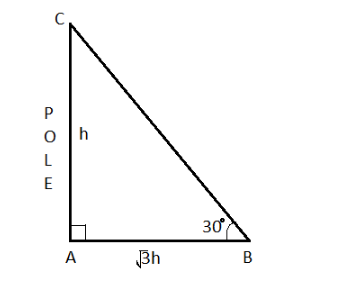
Let us consider AB be the ground surface, AC be the pole as shown in the above figure.
Given that- the height of the pole be $= h\,{\text{m}}$
The shadow of the pole is $= \sqrt 3 h\;{\text{m}}$
Use, the tangent function –
Tangent is defined as the ratio of the opposite side to the adjacent side.
$\Rightarrow \tan \theta = \dfrac{{AC}}{{AB}}$
Place the known values in the above relation –
$\Rightarrow \tan \theta = \dfrac{h}{{\sqrt 3 h}}$
Common factor “h” from the numerator and the denominator cancel each other in the above equation.
$\Rightarrow \tan \theta = \dfrac{1}{{\sqrt 3 }}$
Make the required angle the subject –
$\Rightarrow \theta = {\tan ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right)$
We know that- $\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}$ place the value in the above equation –
$\Rightarrow \theta = {\tan ^{ - 1}}\left( {\tan 30^\circ } \right)$
Inverse of tangent and tangent cancel each other.
$\Rightarrow \theta = 30^\circ$
Hence, the angle of elevation of the Sun is $30^\circ$

Note : Know the difference between the angle of elevation and the angle of depression and apply accordingly. Draw the diagram properly with the given conditions then rest goes well. Please remember all the different trigonometric angles which are the angles given by the ratios of the trigonometric functions. The most important trigonometric angles are $0^\circ ,{\text{ 3}}0^\circ ,\;45^\circ ,{\text{ 6}}0^\circ {\text{ and 9}}0^\circ$ . Remember the values of these angles for quick substitution for further simplification.