Question

Find the angle of elevation of the sun when the length of the shadow of a person is equal to $\sqrt 3$ times his height.

Answer 1

Assume the height of a person to be any variable. Then we can find the length of shadow in terms of that variable. Then draw a right angle triangle as the height of the triangle represents height of person and base of triangle represents length of shadow. Finally we find the angle of elevation by dividing a person's height by the length of shadow.

Formula used: $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$

Complete step-by-step solution:
Assume the height of a person to be any variable.
Let the height of the person be x.
Now we have to find the length of shadow in terms of x.
As it is stated that the length of the shadow of a person is equal to $\sqrt 3$ times of his height
So, the length of shadow is $\sqrt 3 x$.
Draw a right angle triangle as the height of the triangle represents height of person and base of triangle represents length of shadow.

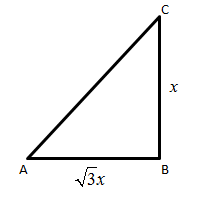
Let $\theta$ be the angle between AC and AB.
As we say that angle of elevation is the upward angle it is from the horizontal to the line of sight from the observer to some point of interest.
So, $\theta$ is the angle of elevation, this is we have to find.
From the diagram, we can observe that if we divide BC by AB, x will cancel out and we will get a number.
So, we find $\tan \theta$ as $\tan \theta = \dfrac{{{\text{Height to }}\angle \theta }}{{{\text{Base to }}\angle \theta }}$.
From the diagram, $\tan \theta = \dfrac{{{\text{BC}}}}{{{\text{AB}}}}$.
Put the value of BC and AB.
$\tan \theta = \dfrac{x}{{\sqrt 3 x}}$
Cancel x from numerator and denominator.
$\tan \theta = \dfrac{1}{{\sqrt 3 }}$
As $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$
$\therefore \theta = {30^ \circ }$
i.e., angle of elevation, $\theta = {30^ \circ }$.
Thus, the angle of elevation of the sun when the length of the shadow of a person is equal to $\sqrt 3$ times his height is ${30^ \circ }$.

Note: Let AB be a vertical line drawn from B to A to meet the horizontal line drawn from O (which is at a lower level than B) and let BO’ be the horizontal line drawn through B (i.e., BO’ is parallel to OA).

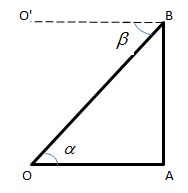
Then $\angle$ AOB is called the angle of elevation of point B as seen from point O and $\angle$ O’BO is the angle of depression of point O as seen from point B. It can be readily seen that $\alpha = \beta$ i.e.
Angle of elevation = Angle of depression (since AO is parallel to BO’)
Using the trigonometric ratios on angle of elevation and depression, we can find out heights and distances.