Question

Find the angle between two tangents drawn to the parabola $y = {x^2}$ from the point (0 ,-2).

Answer 1

Hint:- We should have knowledge that equation of pair of tangent is $S{S_1} = {T^2}$ and also have knowledge that angle between two lines with slope ${m_1}$ and ${m_2}$ is $\alpha = {\tan ^{ - 1}}\left| {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right|$.

Complete step-by-step answer:
We have
Parabola: $y = {x^2}$
We have to draw tangent from (0 ,-2)

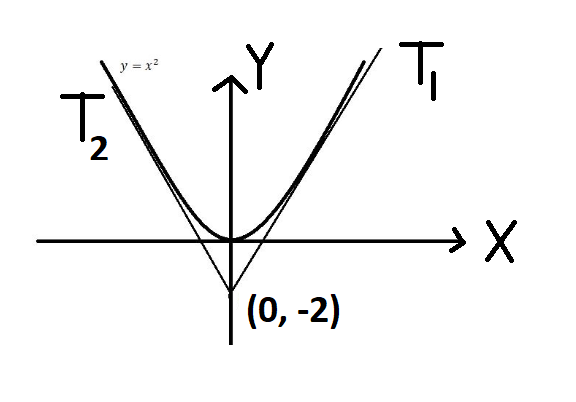
We know formulae of equation pair of tangents from a point is $S{S_1} = {T^2}$
Where $S$ is the equation of curve given and ${S_1}$ is the equation obtained when we put a given point in the equation of curve from where we have to draw a pair of tangents. T is the equation of tangent to the curve from that given point.
Now putting the value of all terms in formula $S{S_1} = {T^2}$ we get,
Here for writing equation of tangent we should know shortcut as like we write $\left( {y = \dfrac{{y + {y_1}}}{2},{x^2} = x{x_1}} \right)$
We use these shortcuts for writing the equation of tangent to a curve where ${x_1},{y_1}$ are the points from which the tangent has to be drawn.
$\left( {\therefore T = x.0 - \dfrac{{\left( {y - 2} \right)}}{2} = - \dfrac{{\left( {y - 2} \right)}}{2}} \right)$
$\Rightarrow \left( {{x^2} - y} \right)\left( {0 - \left( { - 2} \right)} \right) = {\left[ {0 - \dfrac{{\left( {y - 2} \right)}}{2}} \right]^2}$
$\Rightarrow 4\left( {2{x^2} - 2y} \right) = {y^2} + 4 - 4y$
$\Rightarrow 8{x^2} - 4y - {y^2} - 4 = 0 \\\ \Rightarrow 8{x^2} - \left( {{y^2} + 4y + 4} \right) = 0 \\\ \Rightarrow 8{x^2} - {\left( {y + 2} \right)^2} = 0 \\\$
Now use the formulae $\left( {{a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)} \right)$
$\Rightarrow \left( {2\sqrt 2 x - y - 2} \right)\left( {2\sqrt 2 x + y + 2} \right) = 0$
So equations of tangents,
${T_1}:2\sqrt 2 x - y - 2 = 0$ and ${T_2}:2\sqrt 2 x + y + 2 = 0$
Now for slope of a straight line we compare with ( y = mx + c )
Where m is the slope of the line.
Slope of ${T_1} = {m_1} = 2\sqrt 2$
Slope of ${T_2} = {m_2} = - 2\sqrt 2$
Now angle between these tangents, $\alpha = {\tan ^{ - 1}}\left[ {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right]$
$\Rightarrow \alpha = {\tan ^{ - 1}}\left| {\dfrac{{2\sqrt 2 + 2\sqrt 2 }}{{1 - 8}}} \right|$=${\tan ^{ - 1}}\left( {\dfrac{{4\sqrt 2 }}{7}} \right)$

Note: Whenever we get this type of question the key concept of solving is you have to write an equation of pair of tangents and from that equation we have to find slope of the tangents and then using formula find angle between tangents.