Question
Question: Find the angle between the lines \(x + y + 1 = 0\) and \(x = 5\)...
Find the angle between the lines x+y+1=0 and x=5
Solution
We will begin by calculating slope of the lines using the formula −ab, when the equation of line is ax+by+c=0. Then, we will find the angle θ between the lines by plotting the graph of the lines and using the condition m=tanθ, where m is the slope and θ is the angle between the line and the x axis. We will use various properties of angles and sum of triangles to find required angles.
Complete step-by-step answer:
First of all, we will find the slope of the lines x+y+1=0 and x=5.
We know that the slope of any line ax+by+c=0 is given as −ab
Here the slope of line x+y+1=0 will be 1−1=−1
And the slope of the line x=5 is 01,
Since, the slope is undefined.
We will plot the graph of the equations and then find the required angle.
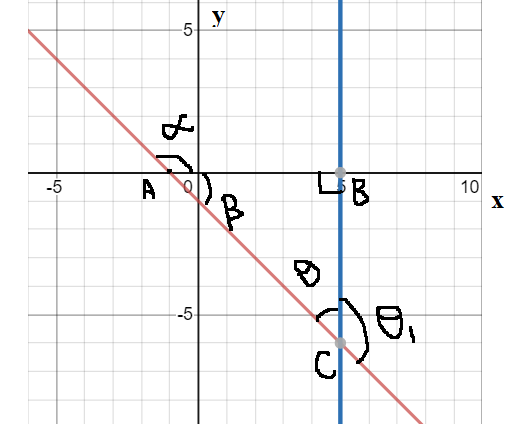
We have to find the angle θ, that is the line x+y+1=0 and x=5.
Here, the α is the angle between the line and thexaxis.
Then, tanα=m , where m is the slope of the line.
Therefore, tanα=−1
Then, α=43π
Also, we know that angles on the same line are supplementary to each other.
Hence, α+β=π
On substituting the value of α=43π in the above equation, we will get,
43π+β=π ⇒β=4π
And the sum of all angles of triangle ABC should be 180∘ which is π.
Hence,
2π+β+θ=π ⇒2π+4π+θ=π ⇒θ=π−(43π) ⇒θ=4π
Hence, the angle between the lines x+y+1=0 and x=5 is 4π.
The angle θ1 will also be the angle between the given lines.
And θ and θ1 are supplementary angles, therefore,
θ+θ1=π ⇒4π+θ1=π ⇒θ1=43π
Thus, the angle between the lines x+y+1=0 and x=5 is 4π or 43π.
Note: The slope of the line which is parallel to they axis is not defined and the slope of the line which is parallel to x axis is 0. Whenever two lines intersect, four angles are formed out of which two pairs are always equal. The value of angles is such that they form a supplementary pair.
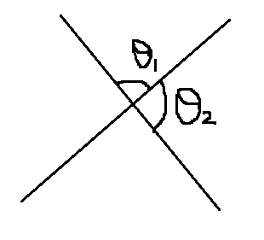
θ1+θ2=π
Angle θ between the lines using the formula, tanθ=1+m1m2m1−m2, where m1 and m2 are slopes of two lines.
