Question

Find the angle between the lines joining the points $\left( { - 1,2} \right),\left( {3, - 5} \right)\,\,\,and\,\,\left( { - 2,3} \right),\left( {5,0} \right)$ .

Answer 1

Hint : To find the angle between two line which passes through two different points. We first find slope of both lines using two point slope formula and then using values of these slopes in formula to find angle between two given lines.
Slope of a line from two points given as: $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
Angle between two lines given as: \tan \theta = \pm \begin{array}{*{20}{c}} \ {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}}\ \end{array}

Complete step-by-step answer :
Given two lines passes through points $\left( { - 1,2} \right),\left( {3, - 5} \right)\,\,\,and\,\,\left( { - 2,3} \right),\left( {5,0} \right)$ .
Calculating slope of lines.

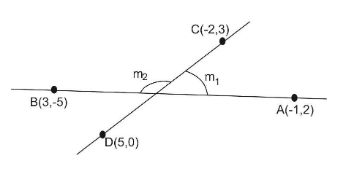
First line passes through points $\left( { - 1,2} \right)\,\,and\,\,\left( {3, - 5} \right)$ .
We know that slope of line passing through two points given as: $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
Which implies slope of firsts line $({m_1}) = \dfrac{{ - 5 - 2}}{{3 - ( - 1)}}$ or
${m_1} = \dfrac{{ - 7}}{{3 + 1}} \\\ \Rightarrow {m_1} = \dfrac{{ - 7}}{4} \\\$
Second line passes through points $( - 2,3)\,\,and\,\,(5,0)$
We know that slope of line passing through two points given as: $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
Which implies slope of second line $({m_2}) = \dfrac{{0 - 3}}{{5 - ( - 2)}}\,\,or$
${m_2} = \dfrac{{ - 3}}{{5 + 2}} \\\ \Rightarrow {m_2} = \dfrac{{ - 3}}{7} \\\$
Also, we know that angle between two lines is given by formula: \tan \theta = \pm \begin{array}{*{20}{c}} \ {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}}\ \end{array}
Substituting values of ${m_1}\,\,and\,\,{m_2}$ calculated above in above formula to find angle between two lines.

\ {\dfrac{{\left( { - \dfrac{7}{4}} \right) - \left( { - \dfrac{3}{7}} \right)}}{{1 + \left( { - \dfrac{7}{4}} \right)\left( { - \dfrac{3}{7}} \right)}}}\ \end{array}$$ $ \Rightarrow \tan \theta = \begin{array}{*{20}{c}} \ {\dfrac{{ - \dfrac{7}{4} + \dfrac{3}{7}}}{{1 + \dfrac{3}{4}}}}\ \end{array} $ $ \Rightarrow \tan \theta = \begin{array}{*{20}{c}} \ {\dfrac{{\dfrac{{ - 49 + 12}}{{28}}}}{{\dfrac{{4 + 3}}{4}}}}\ \end{array} $ $ \Rightarrow \tan \theta = \begin{array}{*{20}{c}} \ {\dfrac{{\dfrac{{ - 37}}{{28}}}}{{\dfrac{7}{4}}}}\ \end{array} \\\ \Rightarrow \tan \theta = \begin{array}{*{20}{c}} \ {\dfrac{{ - 37}}{{28}} \times \dfrac{4}{7}}\ \end{array} \\\ \Rightarrow \tan \theta = \begin{array}{*{20}{c}} \ {\dfrac{{ - 37}}{{49}}}\ \end{array} \\\ \Rightarrow \tan \theta = \left( {\dfrac{{37}}{{49}}} \right) \\\ $ Or $ \theta = {\tan ^{ - 1}}\left( {\dfrac{{37}}{{49}}} \right) $ Hence, from above we see that the angle between two given lines is $ {\tan ^{ - 1}}\left( {\dfrac{{37}}{{49}}} \right) $ . **Note** : When two lines intersect at a point. Two angles formed one is acute and other obtuse. These angles can be calculated by substituting values of slope of lines which can be calculated in different ways like angle form, two point form and line form in standard angle formula of two lines. Formula is $ \tan \theta = \pm \begin{array}{*{20}{c}} \ {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}}\ \end{array} $ . Here, the sign of plus and minus stands for acute and obtuse angles formed between given lines.