Question

Find the angle between the curves:
${{x}^{2}}+{{y}^{2}}-4x-1=0$
${{x}^{2}}+{{y}^{2}}-2y-9=0$

Answer 1

If we observe, the equations given in the question are the equations of the circle and we know that for a circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ , the radius is given by $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ , and centre C=(-g,-f). So, we know the centres and radius of each circle, so we can find the distance between the centres using the distance formula. Once we get the distance use the formula $\cos \theta =\dfrac{{{r}_{1}}^{2}+{{r}_{2}}^{2}-{{d}^{2}}}{2{{r}_{1}}{{r}_{2}}}$ , where $\theta$ is the angle between the circles and d is the distance between the centres.

Complete step-by-step answer :
If we observe, the equations given in the question are the equations of the circle because the coefficient of xy is zero and coefficient of ${{x}^{2}}$ and ${{y}^{2}}$ are same.
We know that for a circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ , the radius is given by $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ , and centre C=(-g,-f). So, for the circle ${{x}^{2}}+{{y}^{2}}-4x-1=0$ , the centre is (2,0) and radius is $\sqrt{{{2}^{2}}-\left( -1 \right)}=\sqrt{5}$ .
Also, for the circle ${{x}^{2}}+{{y}^{2}}-2y-9=0$ , centre is (0,1) and radius is $\sqrt{{{1}^{2}}-\left( -9 \right)}=\sqrt{10}$ . So, let us draw a representative diagram of the situation given.

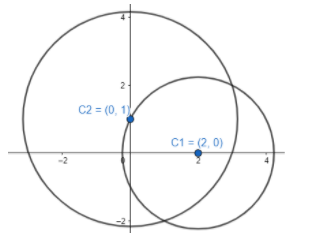
Distance between ${{C}_{1}}\text{ }and\text{ }{{C}_{2}}$ can be found using the distance formula.
Now, according to the distance formula, the distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ is given by $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ .
$\therefore {{C}_{1}}{{C}_{2}}=\sqrt{{{(2-0)}^{2}}+{{(0-1)}^{2}}}=\sqrt{5}$
Now, we know that the distance use the formula $\cos \theta =\dfrac{{{r}_{1}}^{2}+{{r}_{2}}^{2}-{{d}^{2}}}{2{{r}_{1}}{{r}_{2}}}$ , where $\theta$ is the angle between the circles and d is the distance between the centres.
$\cos \theta =\dfrac{{{\left( \sqrt{5} \right)}^{2}}+{{\left( \sqrt{10} \right)}^{2}}-{{\left( \sqrt{5} \right)}^{2}}}{2\sqrt{5}\times \sqrt{10}}=\dfrac{10}{2\times 5\sqrt{2}}=\dfrac{1}{\sqrt{2}}$
Now we know that $\cos 45{}^\circ =\dfrac{1}{\sqrt{2}}$ . So, we can say that the angle between the two circles is $45{}^\circ$ .

Note :If you would not have recognised that the curves are circles then you first have to find the meet point of the curves, then the tangents of both the curves at the meet point and then the angle between the tangents using the formula $\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$ , i.e., the angle between lines. This method is valid for any curve, no matter whether they are standard curves or not.