Question

Find the amount of work that has to be done in assembling three charged particles at the vertices of an equilateral triangle as shown in the figure.

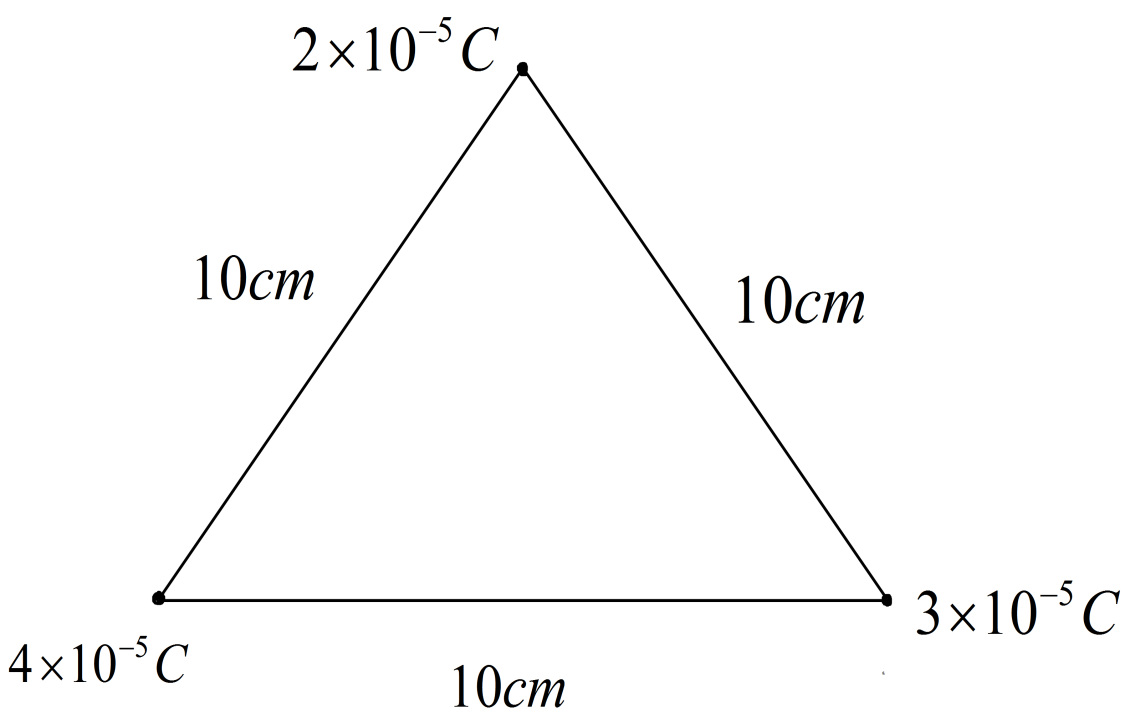
(A) $434J$
(B) $334J$
(C) $234J$
(D) $134J$

Answer 1

Use the formula to find the electrostatic energy to find the work done in assembling the charges. The electrostatic energy of a system of $N$ charges is given by,
$U = \dfrac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{l} j = 1 \\\ j \ne i^N {\dfrac{1}{{4\pi {\varepsilon _0}}}} } \dfrac{{{q_i}{q_j}}}{{{r_{ij}}}}$ . Where, ${r_{ij}}$ is the distance between the charge ${q_i}$ and ${q_j}$ .

Complete Step By Step Answer:
We know that the electrostatic energy due to a system of $N$ charges is given by $U = \dfrac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{l} j = 1 \\\ j \ne i ^N {\dfrac{1}{{4\pi {\varepsilon _0}}}} } \dfrac{{{q_i}{q_j}}}{{{r_{ij}}}}$ . Where, ${r_{ij}}$ is the distance between the charge ${q_i}$ and ${q_j}$ .Here, we have the charges at the vertices of the equilateral triangle that means the distance between the charges are equal.
Now, also we know from work energy theorem, work done on the system is the change in energy of the system. Hence, we can say, the total energy of the system of charges is equal to the work done in assembling the charges.

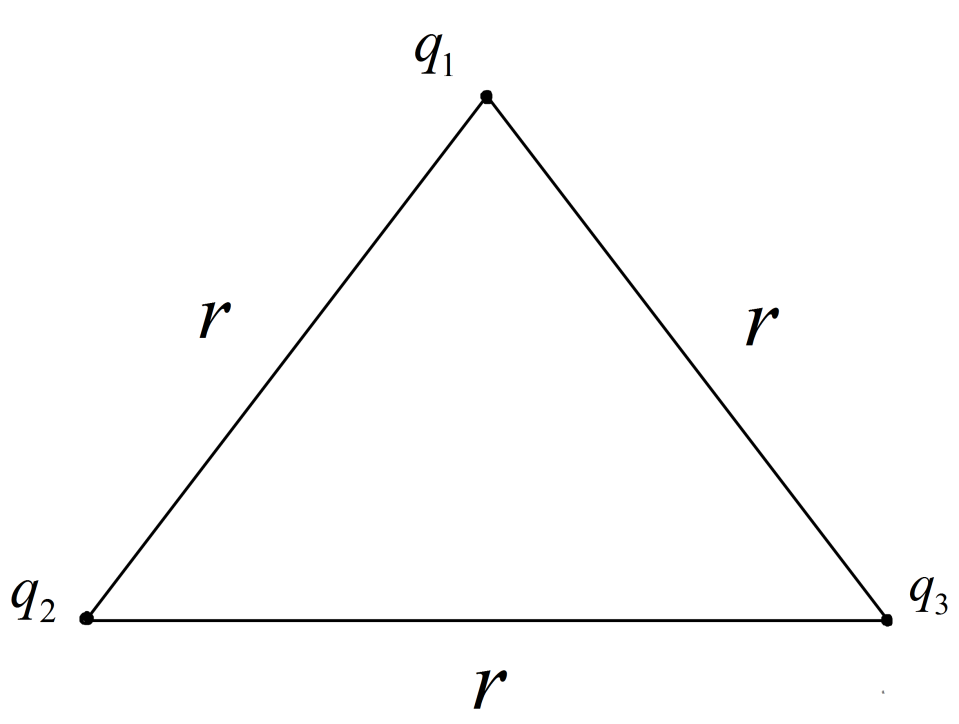
So, we can write work done,
$W = U = \dfrac{1}{2}\sum\limits_{i = 1}^3 {\sum\limits_{l} j = 1 \\\ j \ne i ^3 {\dfrac{1}{{4\pi {\varepsilon _0}}}} } \dfrac{{{q_i}{q_j}}}{{{r_{ij}}}}$ . Since, we have three charges at the vertices.
Now, putting the values of $i$ and $j$ we get, $W = \dfrac{1}{{8\pi {\varepsilon _0}}}[\dfrac{{{q_1}{q_2}}}{r} + \dfrac{{{q_3}{q_1}}}{r} + \dfrac{{{q_2}{q_3}}}{r} + \dfrac{{{q_2}{q_1}}}{r} + \dfrac{{{q_3}{q_1}}}{r} + \dfrac{{{q_3}{q_2}}}{r}]$
Upon simplifying we get, $W = \dfrac{1}{{4\pi {\varepsilon _0}r}}\left[ {{q_1}{q_2} + {q_3}{q_2} + {q_3}{q_1}} \right]$
Putting the values of ${q_1} = 2 \times {10^{ - 5}}C$ , ${q_2} = 4 \times {10^{ - 5}}C$ and ${q_3} = 3 \times {10^{ - 5}}C$ . Distance between the charges $r = 10cm = 0.1m$ we get,
$W = \dfrac{{9 \times {{10}^9}}}{{{{10}^{ - 1}}}} \times \left[ {4 \times 2 \times {{10}^{ - 5}} \times {{10}^{ - 5}} + 4 \times 3 \times {{10}^{ - 5}} \times {{10}^{ - 5}} + 3 \times 2 \times {{10}^{ - 5}} \times {{10}^{ - 5}}} \right]$
On simplifying we get, $W = \dfrac{{9 \times {{10}^9}}}{{{{10}^{ - 1}}}} \times {10^{ - 10}} \times \left( {8 + 12 + 6} \right)$
Or, $W = 9 \times \left( {8 + 12 + 6} \right)$
Or, $W = 9 \times 26 = 234$
Hence, work done in assembling the charges on the equilateral triangle is $234J$ .
Hence, option (C) is correct.

Note:
Here, to assemble the first charge (in bringing the charge from infinity) no energy has been used, since at the beginning there was no force acting on it. Hence, no work needed to be done. The work done to bring the second charge was due to the presence of the first charge and to bring the last charge work was due to the presence of the other two charges.