Question

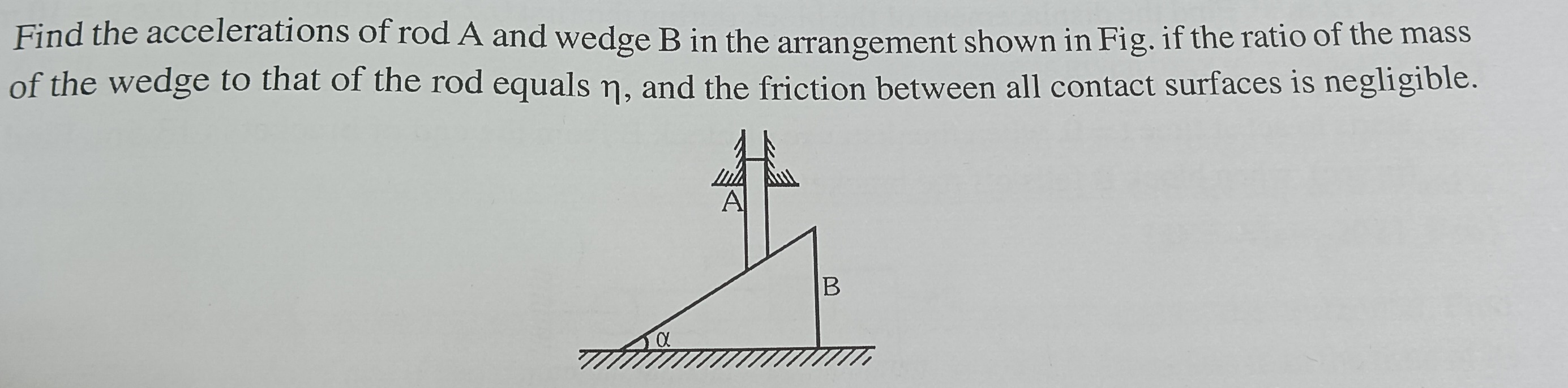
Find the accelerations of rod A and wedge B in the arrangement shown in Fig. if the ratio of the mass of the wedge to that of the rod equals $\eta$, and the friction between all contact surfaces is negligible.

Answer 1

$a_A = \frac{g \sin^2 \alpha}{\sin^2 \alpha + \eta \cos^2 \alpha}, a_B = \frac{g \sin \alpha \cos \alpha}{\sin^2 \alpha + \eta \cos^2 \alpha}$

Answer 2

Let $m$ be the mass of the rod and $\eta m$ be the mass of the wedge. Let $a_A$ be the downward acceleration of the rod and $a_B$ be the horizontal acceleration of the wedge. Due to the contact constraint, $a_A = a_B \tan \alpha$.

Applying Newton's second law to the rod in the vertical direction: $mg - N \cos \alpha = ma_A$, where $N$ is the normal force between the rod and the wedge.

Applying Newton's second law to the wedge in the horizontal direction: $N \sin \alpha = \eta m a_B$.

Solve these three equations for $a_A$ and $a_B$.

From the second equation, $N = \frac{\eta m a_B}{\sin \alpha}$. Substitute this into the first equation: $mg - \frac{\eta m a_B}{\sin \alpha} \cos \alpha = ma_A$.

$g - \eta a_B \cot \alpha = a_A$.

Substitute $a_B = a_A \cot \alpha$: $g - \eta (a_A \cot \alpha) \cot \alpha = a_A$.

$g - \eta a_A \cot^2 \alpha = a_A$.

$g = a_A (1 + \eta \cot^2 \alpha)$.

$a_A = \frac{g}{1 + \eta \cot^2 \alpha} = \frac{g \sin^2 \alpha}{\sin^2 \alpha + \eta \cos^2 \alpha}$.

Then $a_B = a_A \cot \alpha = \frac{g \sin^2 \alpha}{\sin^2 \alpha + \eta \cos^2 \alpha} \frac{\cos \alpha}{\sin \alpha} = \frac{g \sin \alpha \cos \alpha}{\sin^2 \alpha + \eta \cos^2 \alpha}$.

Answer:

The acceleration of rod A is $a_A = \frac{g \sin^2 \alpha}{\sin^2 \alpha + \eta \cos^2 \alpha}$ downwards.

The acceleration of wedge B is $a_B = \frac{g \sin \alpha \cos \alpha}{\sin^2 \alpha + \eta \cos^2 \alpha}$ horizontally to the right.