Question
Question: Find the accelerations \({a_1},{a_2},{a_3}\) of the three blocks shown in figure. If a horizontal fo...
Find the accelerations a1,a2,a3 of the three blocks shown in figure. If a horizontal force of 10N is applied on (i) 2kg block (ii) 7kg block ( Take g=10ms−2). (i.e. find a1,a2,a3 in all three cases).
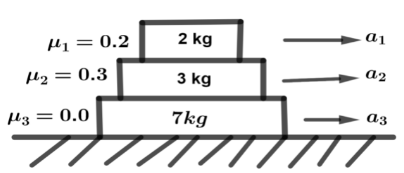
Solution
From the given data there three accelerations a1,a2,a3 in blocks for these accelerations there is some weight on it and some force is acting upon it. For these accelerations there are three cases, now we are going to solve those three cases and here given some value, g=10ms−2. With all those given data we are going to calculate those three accelerations.
Complete step by step answer:
We are going to calculate acceleration in three cases. If any object to move there must be some force that type of force is friction force. By using friction force and applied force only we are going to calculate those three cases. Here given applied force is
F=10N ⇒g=10ms−2
Case 1: For 2kg block
10−f1=2a1
Using frictional force formula, f=μN
10−μ1(2g)=2a1
Already given μ1 value in diagram, by substituting this value we get,
10−0.2×20=2a1 ⇒10−4=2a1 ⇒2a1=6 ∴a1=3ms−2
Case: For 3kg block,
Using same formula,
f1−f2=3a2 ⇒μ1(2g)−μ2(5g)=3a2 ⇒0.2×20−0.3×50=3a2 ⇒3a2=−14 ∴a2=−314
Here we get a2 value in negative which is not possible for acting force on it.
When 3kg and 7kg blocks move together, we have
F1=7a ∴a=74ms−2
Where accelerations a2=a3=74ms−2 are the same.
Now we are going to calculate case (2) in maximum force,
f2max=μ2(5g)=0.3×50=15N ⇒f1max=μ1(2g)=0.2×20=4N
Here the pseudo force is acting on the force which is less than f1max
Now by applying all three forces together, we get
a1=a2=a3=a
This means,
F−m1a=(7+3+2)a ⇒10−2a=12a ⇒14a=10 ∴a=75ms−2
Case3: when all the blocks move together,
a1=a2=a3=a by bringing all blocks, we get
⇒F−m1a−m2a=(7+3+2)a ⇒10−2a−3a=12a ⇒17a=10 ∴a=1710ms−2
In all three cases we have proved the accelerations.
Note: From the given data we have proved it in three cases, in case (1) we have proved the acceleration a1 and acceleration a2 which is not possible. In the second case we have taken the maximum values of force in two types that means f1max and f2max. In the third case we have brought all the blocks together and calculated the acceleration in the joint. Thus we have proven all the three accelerations.
