Question

Find the acceleration of the wedge towards the right so that friction does not act on the block.

Answer 1

We know that for no frictional force to act on the block the relative motion between the wedge and the block should cease to exist. This means that if the block does not move relative to the wedge then we can say that no frictional force is acting on the block.

Formula Used:
We can find the acceleration of the block by using the mathematical formula given below:
$a = g\tan \theta$
In this mathematical formula $g$ represents the acceleration due to gravity and $\theta$ represents the angle of the wedge.

Complete step by step answer:
In the given numerical problem we have to obtain the acceleration of the wedge in the condition that no amount of frictional force acts between the block and the wedge. To fulfil this condition it is important that the relative motion between the wedge and the block should be nil.
For this to happen, the component of all the pseudo-forces along the slope acting on the block must balance the component of gravitational force along the slope. The pseudo forces can be represented using the figure given below:

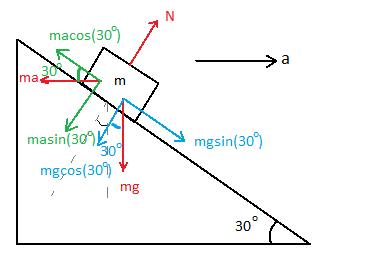
The magnitude of the pseudo-forces is equal to the product of the mass of the block and the acceleration of the block.
From the figure, we can clearly say that:
$ma\cos \theta - mg\sin \theta = 0$
Now the angle of the wedge is given as $30^\circ$. Putting this value in the formula for obtaining the acceleration of the wedge, we obtain:
$a = g\tan 30^\circ$
Now, we already know that $\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}$
Then, substituting this value in the above mathematical expression, we have:
$\Rightarrow a = \dfrac{g}{{\sqrt 3 }}$

Thus, we find that the acceleration of the wedge towards right so that frictional force does not act on the block is equal to $\dfrac{g}{{\sqrt 3 }}$.

Note: Whenever in any numerical problem it is given that the wedge is accelerating, we have to translate every equation into the frame of reference of the wedge. Then by applying pseudo-force we can solve the numerical by taking into consideration the angle of the wedge.