Question

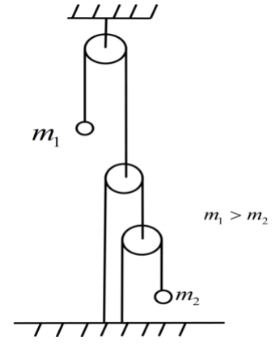
Find the acceleration of the mass ${m_2}$ in the given figure.( Given ${m_1} > {m_2}$, gravitational acceleration $g = 9.8\,m{s^{ - 2}}$ and all the pulleys and strings are massless).

Answer 1

To solve this problem observe the motion of the pulleys when mass ${m_1}$goes downwards. Find the displacement of each pulley for a downward displacement of the mass ${m_1}$. From there, deduce the relation between the acceleration of the mass ${m_1}$ and ${m_2}$. Then find the equation of motion of the mass ${m_2}$using Newton’s law of motion and calculate the acceleration of the mass ${m_2}$ in terms of the mass ${m_1}$and gravitational acceleration.

Formula used:
Equation of motion of a body is given by,
${F_{net}} = ma$
where ${F_{net}}$ is the net force acting on the body, $m$ is the mass of the body and $a$ is the acceleration of the body.
D’Alembert’s principle for equilibrium is given by,
$\sum {F.\delta x} = 0$
where $F$ is the constraint force $\delta x$ is the virtual displacement.

Complete step by step answer:
Here, the only applicable force is the gravitational pull. Now, we have been given that ${m_1} > {m_2}$ and all the pulleys and strings are massless. So, the net acceleration of the mass ${m_2}$ will be upwards. Since, the mass ${m_1}$ will go downwards. Let’s say the displacement of ${m_1}$ is downwards and ${m_2}$ is upwards.

Now, from D'Alembert's principle we know that for equilibrium virtual work done by constraint forces is zero. Here, the constraints forces are the tension in the string. So, the tension on the first string is $T$ on the second string is ${T_1}$ and on the third string it is ${T_2}$ . Now, the tensions on the string are related as, $T = 2{T_1}$ and ${T_1} = 2{T_2}$ by equating the motion of the massless pulleys.

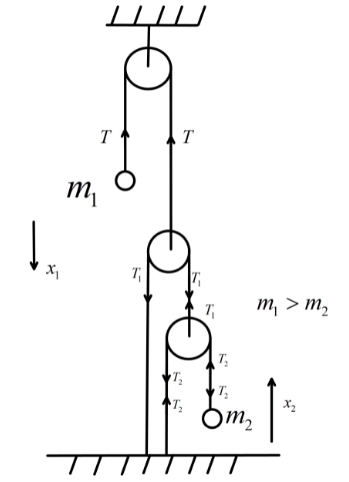
Now, from D’Alembert’s principle we can write,
$- T{x_1} + {T_2}{x_2} = 0$
Putting the value, $T = 4{T_2}$
$4{T_2}{x_1} = {T_2}{x_2}$
$\Rightarrow 4{x_1} = {x_2}$
Further, differentiating we have,
$4{a_1} = {a_2}$
So, we have a relation between the acceleration of the masses.

Now, the equation of motion of the mass ${m_1}$ is,
${m_1}g - T = {m_1}{a_1}$
And, the equation of motion of the mass ${m_2}$ is,
${T_2} - {m_2}g = {m_2}{a_2}$
Putting the value of ${a_2} = 4{a_1}$ and $T = 4{T_2}$ we have,
${m_1}g - 4{T_2} = {m_1}{a_1}$
$\Rightarrow {T_2} - {m_2}g = {m_2}4{a_1}$
Solving these two equation we have,
$\therefore {a_1} = \dfrac{{{m_1} - 4{m_2}}}{{{m_1} + 16{m_2}}}g$

So, the acceleration of the mass ${m_1}$ is $\dfrac{{{m_1} - 4{m_2}}}{{{m_1} + 16{m_2}}}g$ and acceleration of mass ${m_2}$ is, $4\dfrac{{{m_1} - 4{m_2}}}{{{m_1} + 16{m_2}}}g$.

Note: This problem can also be solved by using the fact that string length of each pulley is constant. From there we can differentiate the equation to get the relation between the acceleration of the masses. From there on we can use the equation of motion for each of the masses to find the acceleration of the bodies.