Question

Find the acceleration of the blocks A and B as shown in figure:

$\left( A \right)\dfrac{{10g}}{{13}}forward,\dfrac{{5g}}{{13}}downward$
$\left( B \right)\dfrac{{5g}}{{13}}forward,\dfrac{{10g}}{{13}}downward$
$\left( C \right)\dfrac{{6g}}{{13}}forward,\dfrac{{9g}}{{13}}downward$
$\left( D \right)\dfrac{{9g}}{{13}}forward,\dfrac{{6g}}{{13}}downward$

Answer 1

When objects are connected to strings and a force is applied either vertically or horizontally or along an inclined plane, it produces tension in the string, which affects the acceleration to an extent. Here in the above figure we have a force that is applied vertically and horizontally. Now apply Newton's second law on the body and determine its acceleration.

Complete step by step solution:
Now let us consider the vertical motions acting on the body of mass $5kg$. A gravitational force is acting downwards on the body of mass $5kg$ and a tension $2T$ is acting on a body of mass $5kg$. Now apply Newton's law of motion to determine the forces.

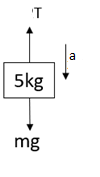
Here we can write the equation using the newton law of motion
$T + 5a - 5g = 0 - - - - - \left( 1 \right)$
Here they tell us the total force acting on the body in the y direction and product of mass and acceleration in the y direction.

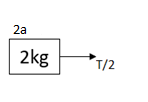
Let’s consider the horizontal motion acting on the body of mass $2kg$.A tension $T$ and acceleration ${a_1}$ is acting on a body of mass $2kg$. Then by applying newton’s law of motion we can write
$4a = \dfrac{T}{2}$
$8a = T - - - - - \left( 2 \right)$
Here the left-hand side tells us the product of mass and acceleration along the x direction and right hand side tells us the net force action in the x direction.
Substitute equation 2 in equation 1 we get
$8a + 5a - 5g = 0$
$a = \dfrac{{5g}}{{13}}$ (Acceleration acting downwards)
Now to acceleration acting upwards, acceleration 2a is acting on mass $2kg$.
$2a = \dfrac{{10g}}{{13}}$ (Acceleration acting forward)

Hence option $\left( A \right)$ is the right option.

Note: For solving problems using newton’s law of motion, free body diagram technique is very useful. The acceleration is affected to an extent when the objects are connected to strings and a force is applied either vertically or horizontally or along an inclined plane. It produces tension in the string. The contact forces arise when a body is in contact with a solid or fluid.