Question

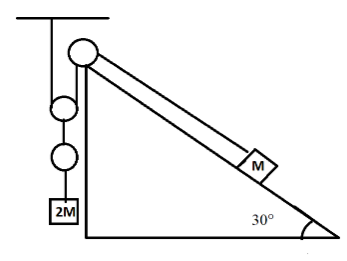
Find the acceleration of the block of mass $M$ in the situation shown in figure. All the surfaces are frictionless and pulleys are massless.

A. $\dfrac{g}{{12}}$
B. $\dfrac{{2g}}{3}$
C. $\dfrac{g}{3}$
D. $\dfrac{g}{4}$

Answer 1

In this question, we are provided with two blocks of mass M and 2M respectively, one is held on to the frictionless surface with the massless pulley. And let the acceleration on the two blocks be $a,\dfrac{a}{2}$ respectively. Wrote the equation of the motion for the two and solved the two equations.

Complete step by step answer:
According to the question, the block of mass M is connected to a massless pulley. Hence, the tension remains unaltered. Let the tension in the string be T, the block of mass M is held on the frictionless surface and the block of mass 2M is connected to a pulley. The block of mass 2M is experiencing the tension 2T due to the pulleys. And now writing the equation of motion for the block placed on the frictionless surface, for that we had made some construction which are shown in the diagram below, where we resolved the components for block of mass M and a be the acceleration,
$T + Ma = Mg\sin 30^\circ$...........................$\ldots \left( 1 \right)$
Now the equation for the block of mass 2M,
$2Mg - 2T = Ma'$..............................$\ldots \left( 2 \right)$

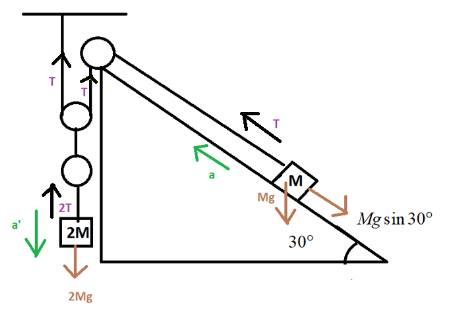
Solving the above marked equations and we know $a' = \dfrac{a}{2}$ ,due to their mass difference as one block is of M and another of 2M. Rewriting the equations,
$T = \dfrac{{Mg}}{2} - Ma \\\ \Rightarrow 2T = 2Mg - \dfrac{{Ma}}{2} \\\$
On solving,
$Mg = \dfrac{{3Ma}}{2} \\\ \therefore a = \dfrac{{2g}}{3} \\\$
Hence, the correct option is B.

Note: Massless pulley is defined as the pulley which does not have rotational inertia that means no force can alter the tension from the string. Frictionless surface means that the block is not experiencing any external force which can be air resistance.