Question

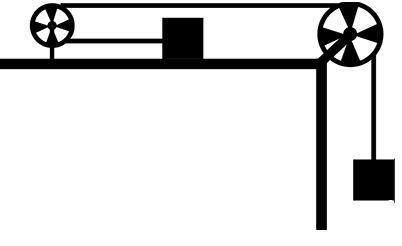
Find the acceleration of either blocks and tension in the string as shown in the figure. It is given that the mass of each block is $m$. The pulley and string are light and all surfaces are smooth.

Answer 1

Calculate the expression for horizontal motion for a block and then calculate the expression for vertical motion from another block then, put the values from one equation into the another and calculate the expressions for acceleration then by using this expression of acceleration find the expression for tension in the string.

Complete step by step answer:
Now, in the question –
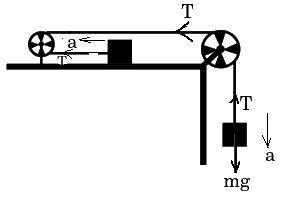
Let the tension in the rope be $T$ and acceleration of the block be $a.$

Now, according to the question, it is given that –
Mass of each block is $m$
For the horizontal motion of the block –
From the figure, we can conclude that the acceleration produced by the horizontal block is $a$ as it is not freely falling the acceleration due to gravity is zero.
Therefore,
$T = ma + m \times 0 \\\ T = ma \cdots (1) \\\$
For the vertical motion of the block –
From the figure, as the vertical block is freely falling so, the acceleration due to gravity is $g$ and acceleration produced is $a.$
Therefore,
$ma = mg - T \cdots (2)$
Putting the value of tension from equation $(1)$ in equation $(2)$, we get –
$ma = mg - ma \\\ 2ma = mg \\\$
Cancelling $m$ on both sides, we get –
$a = \dfrac{g}{2}$
Therefore, we got the expression for acceleration of the block.
Now, in equation $(1)$, using the value of acceleration, we get
$T = m \times \dfrac{g}{2} \\\ T = \dfrac{{mg}}{2} \\\$
This is the required expression for tension in the string.

Note: The force along the length of medium is called the tension. It is especially carried out by flexible mediums such as rope or cable. The tension on an object is the summation of product of mass of object and gravitational force and product of mass and acceleration.