Question
Question: Find the acceleration of \(3\;kg\) mass when acceleration of \(2\;kg\) mass is \(2\;ms^{-1}\) as sho...
Find the acceleration of 3kg mass when acceleration of 2kg mass is 2ms−1 as shown in figure.
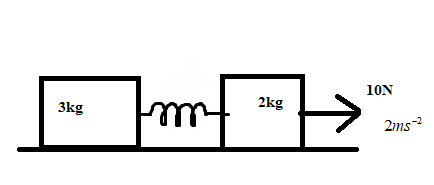
Solution
Here, since the two blocks are attached by a spring, the spring also experiences a tension, which affects the net force on the system of blocks. Using this knowledge we can solve the following question.
Formula used:
F=ma
Complete answer:
Consider the given set-up, where two blocks of different weights are connected by a spring. Thus the net force on the system is the vector sum of the extra force, tension on the spring and the forces acting on the blocks.
Now, consider the2kg block alone, clearly the force action on the 2kg block is given as
A−T=F2 where T is the tension on the spring , A=10N is the applied force and F2=ma is the force on the m=2kg block due to an acceleration a=2m/s2.
Though, we are trying to find the sum of force action on the individual blocks, since the tension acts in the opposite direction to the applied force we are subtracting the two.
⟹10−T=2×2
⟹10−4=T
⟹T=6N
Similarly, now consider the 3kg block alone, then clearly, only T acts on this block, hence we have T=F3 where F3=ma is the force on the m=3kg block due to an acceleration a
Then we have, T=3×a
⟹a=36
∴a=2m/s2
Thus the 3kg block moves with an acceleration of 2m/s2.
Note:
We know the force and tension are vectors, that is they have both magnitude and direction. Hence when we try to add or subtract two or more vectors, we must also consider the direction of the vector along with their magnitude as done in the above question. From Newton's second law of motion we know that the force exerted by a moving object is given as this is used in the above sum extensively.
