Question

Find ratio of Speed of sound in $H_e$, Me then, $Co_2$ If ratio of pressure and density are same for each gas

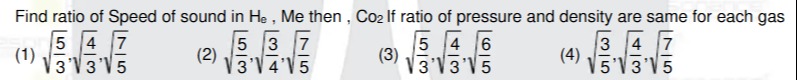
• A. $\sqrt{\frac{5}{3}}.\sqrt{\frac{4}{3}}.\sqrt{\frac{7}{5}}$
• B. $\sqrt{\frac{5}{3}}.\sqrt{\frac{3}{4}}.\sqrt{\frac{7}{5}}$
• C. $\sqrt{\frac{5}{3}}.\sqrt{\frac{4}{3}}.\sqrt{\frac{6}{5}}$
• D. $\sqrt{\frac{3}{5}}.\sqrt{\frac{4}{3}}.\sqrt{\frac{7}{5}}$

Answer 1

Answer: (A)

$\sqrt{\frac{5}{3}} : \sqrt{\frac{4}{3}} : \sqrt{\frac{7}{5}}$

Answer 2

For an ideal gas, the speed of sound is given by

$c = \sqrt{\frac{\gamma\,p}{\rho}}$,

and since $\frac{p}{\rho}$ is the same for all gases, the speed depends only on $\sqrt{\gamma}$.

• Helium (He): $\gamma = \frac{5}{3}$

$\Rightarrow c_{He} \propto \sqrt{\frac{5}{3}}$

• Methane (CH_4) (Me): Being a nonlinear polyatomic molecule, it has 3 translational and 3 rotational degrees of freedom. Thus,

$\gamma = \frac{3+2}{3} = \frac{5}{3}$ is not correct; the proper calculation is through energy considerations which yield $\gamma = \frac{C_p}{C_v} \approx \frac{4}{3}$.

$\Rightarrow c_{Me} \propto \sqrt{\frac{4}{3}}$

• Carbon Dioxide (CO_2): It is a linear molecule with 3 translational and 2 rotational degrees of freedom (vibrations not excited at room temperature), so

$\gamma = \frac{5+2}{5} = \frac{7}{5}$

$\Rightarrow c_{CO_2} \propto \sqrt{\frac{7}{5}}$

Thus, the ratio of the speeds is

$\sqrt{\frac{5}{3}} : \sqrt{\frac{4}{3}} : \sqrt{\frac{7}{5}}$.