Question

Find Principle solution of $\sin 2x + 2 \sin x + 2 \cos x + 1 = 0$

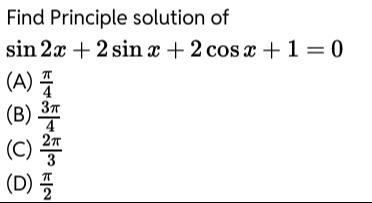
• A. $\frac{\pi}{4}$
• B. $\frac{3\pi}{4}$
• C. $\frac{2\pi}{3}$
• D. $\frac{\pi}{2}$

Answer 1

Answer: (B)

$\frac{3\pi}{4}$

Answer 2

Use $\sin 2x = 2 \sin x \cos x$ to rewrite the equation as $2 \sin x \cos x + 2 \sin x + 2 \cos x + 1 = 0$. Rearrange to $(2 \sin x \cos x + 1) + 2(\sin x + \cos x) = 0$. Recognize $1 + 2 \sin x \cos x = (\sin x + \cos x)^2$. The equation becomes $(\sin x + \cos x)^2 + 2(\sin x + \cos x) = 0$. Let $y = \sin x + \cos x$. This gives $y^2 + 2y = 0$, so $y(y+2)=0$. Thus, $y=0$ or $y=-2$. $y=0 \implies \sin x + \cos x = 0 \implies \tan x = -1 \implies x = n\pi - \frac{\pi}{4}$. $y=-2$ yields no real solutions as the range of $\sin x + \cos x$ is $[-\sqrt{2}, \sqrt{2}]$. For $n=1$, $x = \frac{3\pi}{4}$, which is a principal solution and matches option (B).