Question

Find out the work done by the gas in a cyclic process:

A. $100J$
B. $200J$
C. $600J$
D. $1000J$

Answer 1

Gas is continuously moving and since the gas compresses around its environment when it expands, the work carried out by the gas is equal to the force the gas applies on the environment multiplied by the distance covered. Also change in pressure and volume can be calculated from the graph to find the magnitude of work done.

Complete step by step answer:
Let us understand the given details from the question: a cyclic process is given in the diagram along with the values of pressure and volume at different times. This cycle is said to be a Carnot Cycle since the graph represents the gas’s characteristics of pressure and volume.We are required to compute the work done from the given graph, so we need to establish a relationship between the work performed, pressure and volume.

From the given graph we should be clear that work done is always defined by the area under the graph so the product of change in volume and pressure is the required work done by the gas. The graph in the question has been made according to the values of initial and final volume and pressure of the gas. Let us draw the given diagram again and mark down different points;

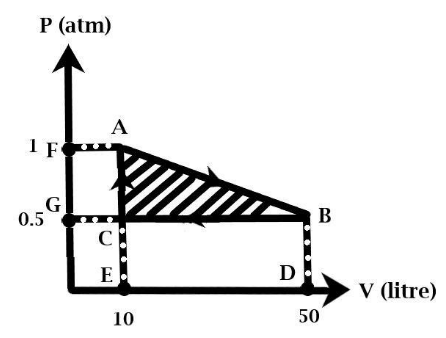
The shaded area that is triangle $ABC$ represents the area under the graph. We see that the triangle is right angled at $\angle ACB$, so the formula for the area of triangle will be:
Area $= \dfrac{1}{2} \times AC \times BC$
This area is equivalent to the work done so let us look at the diagram to draw some relations between the triangle and volume/pressure:
Initial pressure ${P_i} = 0.5\;atm$
Final pressure ${P_f} = 1\;atm$
Now the change in pressure (base of triangle):
$\Delta P = (1 - 0.5)\;atm$
$\Rightarrow \Delta P = AC = 0.5\;atm$
Initial volume ${V_i} = 10\;L$
Final volume ${V_f} = 50\;L$
Now the change in volume (height of triangle):
$\Delta V = (50 - 10)\;L$
$\Rightarrow \Delta V = BC = 40\;L$
If the work done can be computed by the area under the graph it means that the work done here will be:
$\text{work done} = \dfrac{1}{2} \times \Delta P \times \Delta V$ (Since the area of the triangle is the same as the area under the graph.)
$\Rightarrow \text{work done} = \dfrac{1}{2} \times 0.5\;atm \times 40\;L$

Let us convert the units in such a way that we get the standard unit of work done that is $J$.
$\text{work done} = \dfrac{1}{2} \times (0.5\; \times 101.3 \times {10^3})\;Pa \times (40 \times {10^{ - 3}})\;{m^3}$
$\Rightarrow \text{work done} = \dfrac{1}{2} \times (0.5\; \times 101.3)\;Pa \times (40)\;{m^3}$
Simplifying further we get:
$\text{work done} = (0.5\; \times 101.3) \times 20\;J$
$\therefore \text{work done} = 1013\;J$
This value is approximately equal to $\text{work done} \approx 1000\;J$. So therefore the work done can be considered to be $1000\;J$.

Hence, the correct answer is option D.

Note: When we calculate the work done by finding the area under a graph, the graph can take any shape. So sometimes we might need to find the area of a graph that is in the form of a quadrilateral, so in such a case, utilizing the values provided in the graph we can find the area of the quadrilateral.