Solveeit Logo
Login

Question

Question: Find out the correct relation for the dependence of change in acceleration due to gravity on the ang...

Find out the correct relation for the dependence of change in acceleration due to gravity on the angle at latitude due to rotation of Earth.
A. dg α cosθdg{\text{ }}\alpha {\text{ cos}}\theta
B. dg α cos2θdg{\text{ }}\alpha {\text{ co}}{{\text{s}}^2}\theta
C. dg α cos32θdg{\text{ }}\alpha {\text{ co}}{{\text{s}}^{\dfrac{3}{2}}}\theta
D. dg α 1 cosθdg{\text{ }}\alpha {\text{ }}\dfrac{1}{{{\text{ cos}}\theta }}

Explanation

Solution

The two forces that act on the Earth are the force due to gravity and the centrifugal force. Centrifugal force depends on the angle of latitude. So the resultant force changes with the angle of latitude. The resultant acceleration due to these forces is termed as the effective acceleration due to gravity. Derive the relation between effective gravity and angle of latitude by balancing the force to find the dependence of gravity on the angle of latitude.

Complete step by step solution:
On any point on the earth there acts the two forces which are force due to gravity and the centrifugal force due to the rotation of earth. This centrifugal force acts outwards hence decreasing the resultant force.

Let us consider Earth as a sphere of mass MM and radiusRR. Take an object of mass mmat the point P at a latitude with the angleθ\theta . As the earth is rotating the object experiences the centrifugal force along with the force of gravity.

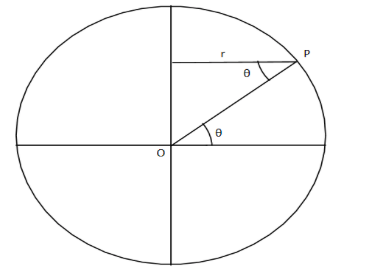
 ![](https://www.vedantu.com/question-sets/ed573334-6129-4aa0-86f3-610184e401548721166356233846904.png)

The object is moving in the circular path if radius rr
The relation between rr and the radius of earth RR is given as
r=Rcos⁡θr = R\cos \theta
So the centrifugal force Fc=mω2r=mω2Rcos⁡θ{F_c} = m{\omega ^2}r = m{\omega ^2}R\cos \theta
Let us represent the resultant acceleration as g′g' or in other words the effective acceleration due to gravity.
Since the force is vector we will use the vector addition here, we get
R2=A2+B2+2ABcos⁡ϕ{R^2} = {A^2} + {B^2} + 2AB\cos \phi
(mg′)2=(mg)2+(mω2Rcos⁡θ)2+2mg.mω2Rcos⁡θcos⁡(180−θ){(mg')^2} = {(mg)^2} + {(m{\omega ^2}R\cos \theta )^2} + 2mg.m{\omega ^2}R\cos \theta \cos (180 - \theta )
m2(g′)2=m2(g)2+m2ω4R2cos⁡2θ+2m2gω2Rcos⁡2θ{m^2}{(g')^2} = {m^2}{(g)^2} + {m^2}{\omega ^4}{R^2}{\cos ^2}\theta + 2{m^2}g{\omega ^2}R{\cos ^2}\theta
(g′)2=(g)2(1+ω4R2cos⁡2θg2−2ω2Rcos⁡2θg){(g')^2} = {(g)^2}\left( {1 + \dfrac{{{\omega ^4}{R^2}{{\cos }^2}\theta }}{{{g^2}}} - \dfrac{{2{\omega ^2}R{{\cos }^2}\theta }}{g}} \right)
For earth the value of angular velocity ω\omega is 7.29×10−57.29 \times {10^{ - 5}} so we will neglect the terms containing ω4{\omega ^4}
So we have
(g′)2=(g)2(1−2ω2Rcos⁡2θg){(g')^2} = {(g)^2}\left( {1 - \dfrac{{2{\omega ^2}R{{\cos }^2}\theta }}{g}} \right)
(g′)=(g)(1−2ω2Rcos⁡2θg)12(g') = (g){\left( {1 - \dfrac{{2{\omega ^2}R{{\cos }^2}\theta }}{g}} \right)^{\dfrac{1}{2}}}
Using the binomial expansion and neglecting the higher power terms we get that
(g′)=(g)(1−12.2ω2Rcos⁡2θg)(g') = (g)\left( {1 - \dfrac{1}{2}.\dfrac{{2{\omega ^2}R{{\cos }^2}\theta }}{g}} \right)
g′=g−ω2Rcos⁡2θg' = g - {\omega ^2}R{\cos ^2}\theta
g−g′=ω2Rcos⁡2θg - g' = {\omega ^2}R{\cos ^2}\theta
For small angle θ\theta g−g′=dgg - g' = dg
So dg=ω2Rcos⁡2θdg = {\omega ^2}R{\cos ^2}\theta
dgαcos⁡2θdg\alpha {\cos ^2}\theta

Option B is correct.

Note: The main key in the question is considering the centrifugal force along with force due to gravity and vector addition of force. Take care while taking the components.