Question

Find order of the differential equation whose solution is given by $x+2x+c_3sin^2(x+c_4)+c_5e^{x+c_6}+lnc_7x+c_8$, is.

Answer 1

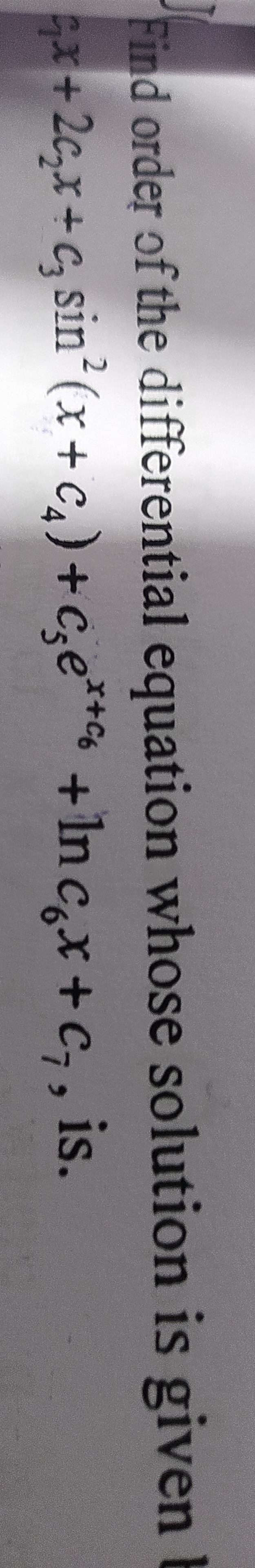
4

Answer 2

The order of a differential equation is equal to the number of independent arbitrary constants in its general solution.

Let the given solution be $y$: $y = x+2x+c_3sin^2(x+c_4)+c_5e^{x+c_6}+lnc_7x+c_8$

First, simplify the expression by combining like terms and properties of exponents and logarithms: $y = 3x + c_3sin^2(x+c_4) + c_5e^x e^{c_6} + lnc_7 + lnx + c_8$

Now, let's identify and simplify the arbitrary constants:

1. $c_3$: This is an independent arbitrary constant.
2. $c_4$: This is an independent arbitrary constant.
3. $c_5e^{c_6}$: This combination of two constants ($c_5$ and $c_6$) can be represented as a single independent arbitrary constant. Let $A = c_5e^{c_6}$.
4. $lnc_7$: This is a constant.
5. $c_8$: This is a constant.

The terms $lnc_7$ and $c_8$ are additive constants. They can be combined into a single independent arbitrary constant. Let $B = lnc_7 + c_8$.

So, the general solution can be rewritten as: $y = 3x + c_3sin^2(x+c_4) + Ae^x + lnx + B$

Now, let's list the independent arbitrary constants present in this simplified general solution:

1. $c_3$
2. $c_4$
3. $A$ (which represents $c_5e^{c_6}$)
4. $B$ (which represents $lnc_7 + c_8$)

There are 4 independent arbitrary constants in the given general solution. Therefore, the order of the differential equation is 4.