Question

Find number of solutions of the equation $\sin x={{x}^{2}}+x+1$ .

Answer 1

Hint : To solve the question given above, we will first find out the range of the function $f\left( x \right)={{x}^{2}}+x+1$ . To find the range, we will find out its maximum value and minimum value as infinite and for an equation $a{{x}^{2}}+bx+c=0\ as\ -\left( \dfrac{{{b}^{2}}-4ac}{4a} \right)$ . Then, we will find out at what x, $f\left( x \right)$ us minimum using $x=\dfrac{-b}{2a}$ . Then, at that value of x, we will check whether the $\sin x$ is more than the minimum value of $f\left( x \right)$ or not. On this basis, we will determine how many solutions are there for the above equations.

Complete step-by-step answer :
To start with, we will first find out the range of the function $f\left( x \right)={{x}^{2}}+x+1$ . Now, to find the range of $f\left( x \right)$ we will find its maximum value and minimum value. We can clearly see that the maximum value of $f\left( x \right)$ will be infinite. Now, we know that the minimum value of the equation $a{{x}^{2}}+bx+c=0\ as\ -\left( \dfrac{{{b}^{2}}-4ac}{4a} \right)$ . In our case, a = 1, b = 1 and c = 1. Thus, minimum value of $f\left( x \right)=-\left( \dfrac{{{\left( 1 \right)}^{2}}-4\left( 1 \right)\left( 1 \right)}{4} \right)$ . Thus, the minimum value of $f\left( x \right)=\dfrac{-3}{4}$ . Now, the minimum value of $f\left( x \right)$ occurs at $x=\dfrac{-b}{2a}$ . Thus, $x=\dfrac{-1}{2}$ . Thus, the rough graph of $y={{x}^{2}}+x+1$ is:

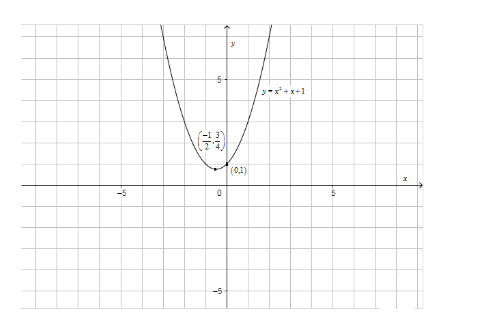
Now, we have to determine the value of $\sin x$ at $x=\dfrac{-1}{2}$ . We know that in $\left[ \dfrac{-\pi }{2},0 \right)$ , $\sin x$ is negative i.e. it is not possible for $\sin x$ to interest $f\left( x \right)$ in that interval. Also, the maximum value of $\sin x$ is 1. Thus, the combined graph of $y=\sin x\ and\ y={{x}^{2}}+x+1$ is shown below:

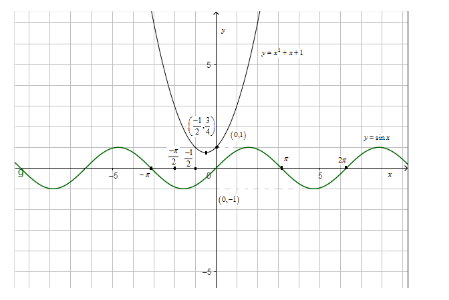
Thus, we can see that both the graphs do not intersect at all. Thus, there will be no solution of $\sin x={{x}^{2}}+x+1$ .
Hence, there are 0 solutions of the equation $\sin x={{x}^{2}}+x+1$ .

Note : he minima of $f\left( x \right)={{x}^{2}}+x+1$ can also be find out by an alternate method as shown below:
We know that if $f\left( x \right)$ is a quadratic function of the form $a{{x}^{2}}+bx+c$ , where $a>0$ then its minimum value will occur at $x=\alpha$ where $\alpha$ is solution of $f'\left( x \right)=0$ . Thus, we have:
$f\left( x \right)={{x}^{2}}+x+1$
On differentiating both sides, we have:
$\Rightarrow f'\left( x \right)=2x+1$
Now, $f'\left( x \right)=0$ . So, we have
$\begin{aligned} & \Rightarrow 2x+1=0 \\\ & \Rightarrow x=\dfrac{-1}{2} \\\ \end{aligned}$
At $x=\dfrac{-1}{2}$ , there will be minima. The value of this minima will be $=f\left( \dfrac{-1}{2} \right)$ . Thus,
$\begin{aligned} & f\left( \dfrac{-1}{2} \right)={{\left( \dfrac{-1}{2} \right)}^{2}}+\left( \dfrac{1}{2} \right)+1 \\\ & f\left( \dfrac{-1}{2} \right)=\dfrac{-3}{4}+\dfrac{3}{2}=\dfrac{3}{4} \\\ \end{aligned}$