Question
Question: Find minimum value of w so that particle strikes P P (30,40) ...
Find minimum value of w so that particle strikes P P (30,40)
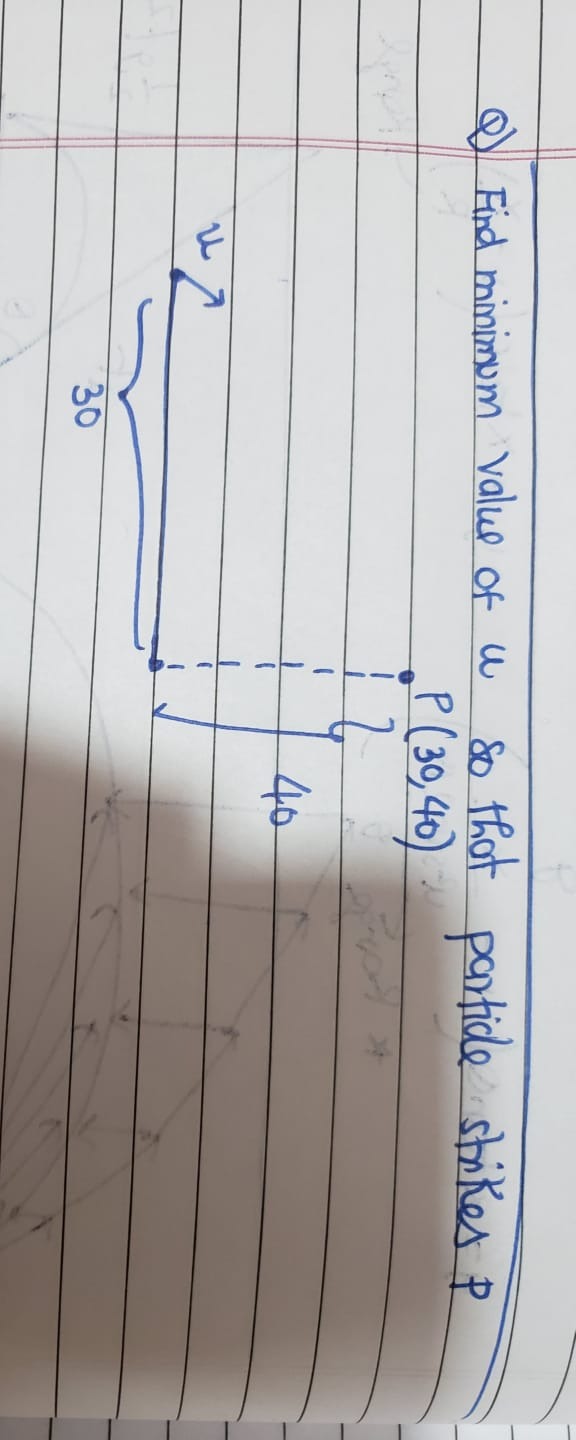
30
Solution
The problem asks for the minimum value of u (represented as w in the question text) such that a particle strikes point P(30,40). We assume the particle is launched from the origin (0,0) with initial velocity u at an angle theta with the horizontal. The diagram provided is somewhat ambiguous, but when specific coordinates P(30,40) are given, they take precedence.
The equation of trajectory for a projectile launched from the origin (0,0) with initial velocity u at an angle theta with the horizontal is:
y = x \tan\theta - \frac{g x^2}{2 u^2 \cos^2\theta}
We are given the target point P(x, y) = (30, 40). Substitute these values into the trajectory equation:
40 = 30 \tan\theta - \frac{g (30)^2}{2 u^2 \cos^2\theta}
40 = 30 \tan\theta - \frac{900g}{2 u^2 \cos^2\theta}
40 = 30 \tan\theta - \frac{450g}{u^2 \cos^2\theta}
We can rewrite \frac{1}{\cos^2\theta} as \sec^2\theta = 1 + \tan^2\theta:
40 = 30 \tan\theta - \frac{450g}{u^2} (1 + \tan^2\theta)
To find the minimum value of u, we need to express u^2 in terms of \tan\theta and then minimize u^2 with respect to \tan\theta.
Let T = \tan\theta.
40 = 30T - \frac{450g}{u^2} (1 + T^2)
Rearrange the equation to solve for u^2:
\frac{450g}{u^2} (1 + T^2) = 30T - 40
u^2 = \frac{450g (1 + T^2)}{30T - 40}
For u to be real, u^2 must be positive. Since g > 0 and (1 + T^2) > 0, we must have 30T - 40 > 0, which implies 30T > 40, or T > 4/3.
To find the minimum u^2, we differentiate u^2 with respect to T and set the derivative to zero. Let f(T) = \frac{1 + T^2}{30T - 40}.
\frac{df}{dT} = \frac{(2T)(30T - 40) - (1 + T^2)(30)}{(30T - 40)^2}
Set the numerator to zero:
2T(30T - 40) - 30(1 + T^2) = 0
60T^2 - 80T - 30 - 30T^2 = 0
30T^2 - 80T - 30 = 0
Divide by 10:
3T^2 - 8T - 3 = 0
Solve this quadratic equation for T using the quadratic formula T = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}:
T = \frac{-(-8) \pm \sqrt{(-8)^2 - 4(3)(-3)}}{2(3)}
T = \frac{8 \pm \sqrt{64 + 36}}{6}
T = \frac{8 \pm \sqrt{100}}{6}
T = \frac{8 \pm 10}{6}
Two possible values for T:
T_1 = \frac{8 + 10}{6} = \frac{18}{6} = 3
T_2 = \frac{8 - 10}{6} = \frac{-2}{6} = -\frac{1}{3}
We established the condition T > 4/3.
T_1 = 3 satisfies 3 > 4/3.
T_2 = -1/3 does not satisfy -1/3 > 4/3.
Therefore, the valid value for T (i.e., \tan\theta) that minimizes u is T = 3.
Now substitute T = 3 back into the expression for u^2:
u^2 = \frac{450g (1 + 3^2)}{30(3) - 40}
u^2 = \frac{450g (1 + 9)}{90 - 40}
u^2 = \frac{450g (10)}{50}
u^2 = \frac{4500g}{50}
u^2 = 90g
Assuming the acceleration due to gravity g = 10 m/s^2 (a common approximation in such problems unless specified otherwise):
u^2 = 90 \times 10
u^2 = 900
u = \sqrt{900}
u = 30 m/s
The minimum value of u (or w) is 30 m/s.
