Question

Find median of the following grouped data graphically?

Class Interval	Frequency
0-5	03
5-10	06
10-15	11
15-20	08
20-25	06

Answer 1

First we will write the definition of the median in general and then we will write the given data and then we will make a more than curve and a less than curve by first making a more than cumulative frequency table and a less than cumulative frequency table, finally we will plot the obtained points and then where the two points intersect that will be our median.

Complete step by step answer:
First let’s understand the meaning of the median of a given data, so median is the middle value of the given set of data when arranged in a particular order. Now, if the number of observations in any given data is odd, therefore the median will be ${{\left( \dfrac{n+1}{2} \right)}^{th}}$term, whereas when the number of observations is even then the median will be both ${{\left( \dfrac{n}{2} \right)}^{th}}\text{ and }{{\left( \dfrac{n}{2}+1 \right)}^{th}}$ observations.
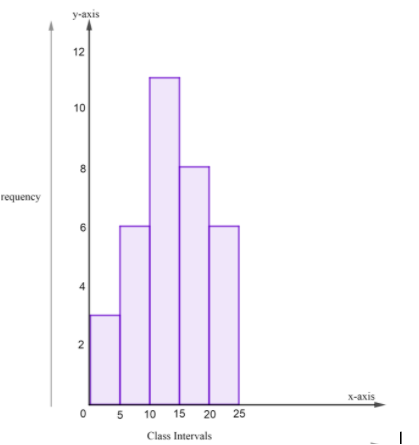
So, let’s consider the data given to us:

Class Interval	Frequency
0-5	03
5-10	06
10-15	11
15-20	08
20-25	06

Graphical representation for above data will look like the following figure:

Similarly, we will form less than cumulative frequency table, that means we will take the upper limit of every class and see what is the total frequency present before that, which will be our cumulative frequency:

Class Interval	Cumulative Frequency
Less than 5	3
Less than 10	9
Less than 15	20
Less than 20	28
Less than 25	34

We will now plot these cumulative frequencies on a graph and form a more than curve and a less than curve and we know that the point where more than and less than curves meet then that will be our median.

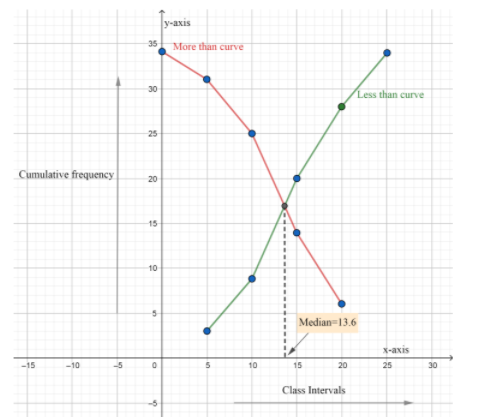
As, we see from the graph that more than and less than curve meets at 13.6 therefore, the median is 13.6

Note: Since, it is a grouped data conventional formula for median is not applied. For calculating the median of a grouped data, following formula is applied:
$\text{Median}=L+\dfrac{\left( \dfrac{n}{2} \right)-B}{G}\times w$
Where, L is the lower class boundary of the group containing the median, n is the total number of values, B is the cumulative frequency of the groups before the median group, G is the frequency of the median group and w is the group width.