Question

Find maximum acceleration of a monkey of mass $5kg$, so that the block remains stationary.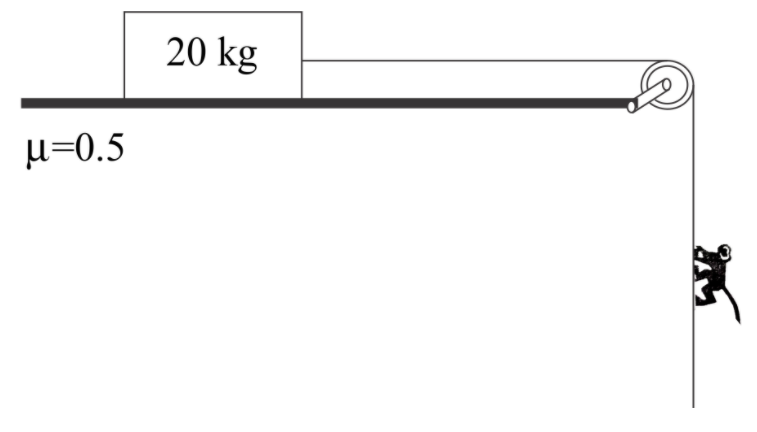

A) $5m{s^{ - 2}}$
B) $10m{s^{ - 2}}$
C) $20m{s^{ - 2}}$
D) $6.67m{s^{ - 2}}$

Answer 1

The block has to remain stationary, which means the net force on the block will be zero. So, the friction force should be working at its maximum on the block, that will be opposing the motion of the block in forward direction, which is due to the tension created in the string due to the motion of the monkey.

Complete step by step answer:
Maximum friction force $fr$ acting on the block in backward direction is $\mu N$
Where $\mu$ is coefficient of friction and
$N$ is a normal reaction of the block.
And $N = mg$
Where $m$ is mass of block and $g$ is gravity.
So, $fr = \mu mg$
Using values given in question, we get
$fr = 0.5 \times 20 \times 10$
On solving this we get
$fr = 100N$
Now, the force acting on the block in forward direction ( $F$ ) is the force by which the rope is pulling the block in forward direction. And the force by which rope is pulling is the sum of weight of monkey and the force by which monkey is pulling rope, that is, mass of monkeys times it’s upward acceleration.
So, $F = {m_{monkey}}g + {m_{monkey}}a$
Where $a$ is maximum acceleration by which monkey can move upwards so that the block doesn’t move.
Using values given in question we get,
$F = 5 \times 10 + 5 \times a$
On solving, we get,
$F = 50 + 5a$
Now, $F = fr$ So that net force on the block is zero, that is, block doesn’t move.
So, we get
$50 + 5a = 100$
On further solving we get,
$a = 10m{s^{ - 2}}$
So, the maximum acceleration by which monkey can move upward so that the block doesn’t move is $10m{s^{ - 2}}$
Hence the correct answer is option (B)

Note: The force by which rope is pulling is the sum of weight of monkey and the force by which monkey is pulling rope because the weight of monkey and monkey pulling force on the rope will be both in downward direction and this whole force is applied to rope in downward direction.