Question
Question: Find linear expression of $\sin^{-1}(\sin x)$ for $x \in [\frac{2025\pi}{2},\frac{2027\pi}{2}]$...
Find linear expression of sin−1(sinx) for x∈[22025π,22027π]
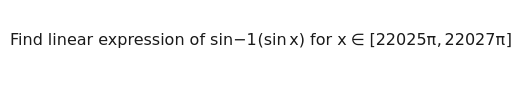
Answer
1013π - x
Explanation
Solution
-
Use the formula sin−1(sinx)=(−1)n(x−nπ) for x∈[nπ−2π,nπ+2π].
-
For x∈[22025π,22027π], set nπ−2π=22025π to get n=1013.
-
Since 1013 is odd, (−1)1013=−1.
-
Thus, sin−1(sinx)=−(x−1013π)=1013π−x.
